Hongbo Ma's Blog

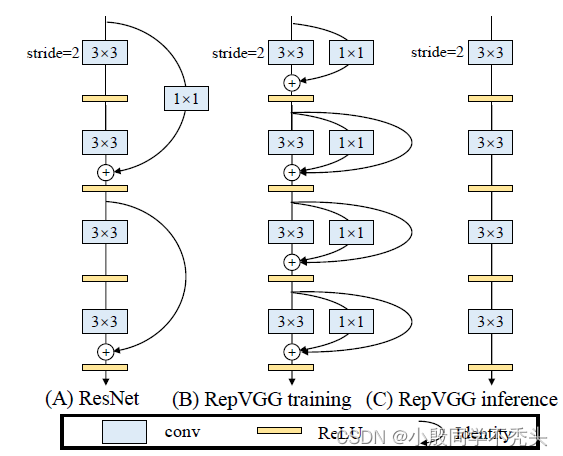
重参数化 PDF中不含参数求函数期望的梯度 由期望的积分定义： 可以将求导号移入积分： 这个形式下可以直接使用蒙特卡罗方法进行求解 PDF中含参数求函数期望的梯度 如何解决的计算成为了一个问题 解决方法一： log trick 定义 且对 可微。令 对两边关于 求导（链式法则）： 移项得到 由上述恒等式代入 即 这就是打分函数 score function形式 这个方法具有通用性，但问题是方差很大 解决方法二： 重参数化 常见的目标形式是： 但直接对这个期望求梯度比较麻烦，因为 的分布 依赖于 重参数化的核心思想是把依赖 的随机性转移到一个固定分布的随机变量 上，从而“分离”随机性与参数 即： 与无关 于是期望可以写成： 先证明: 证明完毕后将上述结果代入： 对 求梯度时， 的分布不依赖 ，所以： 这时我们可以 直接对被积函数求导再采样估计，避免了方差巨大的 score function 特点：方差小，但是并不通用

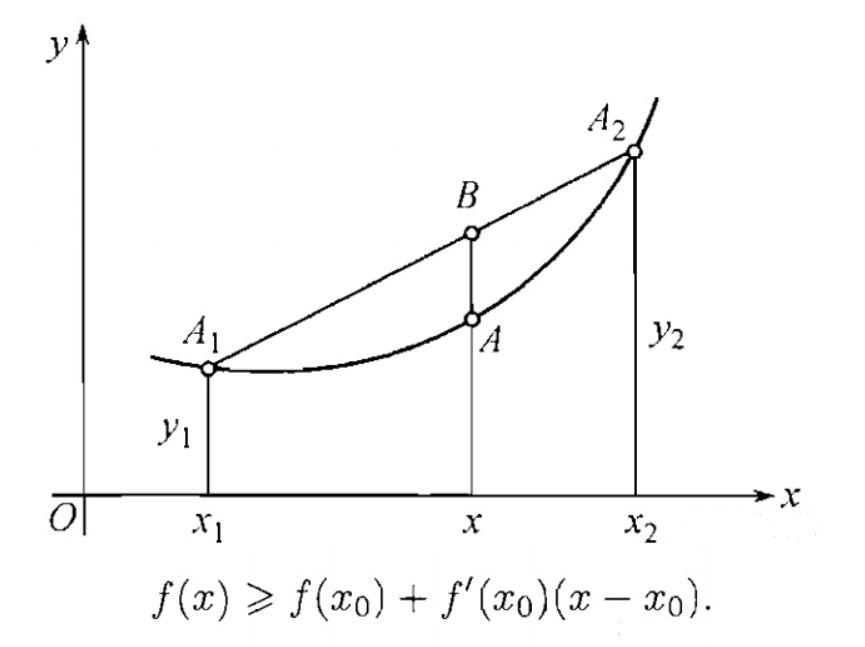
琴生不等式 我们从双变量形式开始，理解琴生不等式 两个变量形式 设 是一个 凸函数。 给定两个点 ，以及一个权重 ，则有： 这就是 琴生不等式在两个变量下的形式 直观几何解释 在平面上取两点 和 连线就是这两点的割线 凸函数的定义就是：函数图像始终在割线之下 左边 表示 先在横坐标上取加权平均，再带入函数 右边 表示 函数值的加权平均 由于曲线在割线下方，所以左边 ≤ 右边 代数证明 设 在区间 上是凸函数。任取 与 ，记 若 凸，则割线斜率单调递增，对任意 有 由 可知 取 (★) 的左右两端不等式，得到 交叉相乘并整理： 这正是 即 多变量形式及随机变量形式 三变量证明 双变量形式为：若 是凸函数，，则 我们先考虑三变量形式：取三个点 ，权重 ，且 欲证： 把三点的凸组合拆成“两点情况的嵌套”，即： 于是 其中 先对 用两点不等式： 再对 应用两点不等式： 代入就得到三变量情况 推广到n变量 假设对 个变量成立： 考虑 个变量： 令 里面的括号是 个变量的凸组合，应用归纳假设： 再对“括号中的点”和...

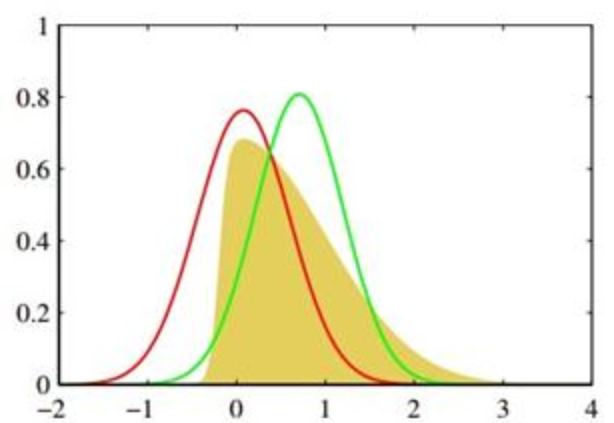
KL散度 KL 散度（Kullback–Leibler divergence）是用来衡量两个概率分布之间差异的一种方法。它的数学表达式和理解可以分几个层次来看： 1. 数学定义 如果我们有两个概率分布 （真实分布）和 （近似分布），它们定义在同一个随机变量 上，则 离散情况下： 或者连续情况下： 2. 核心直觉 非对称性： 所以它不是一个真正的“距离”，而更像是一种有方向的差异测量 非负性 当且仅当 （几乎处处相等）时取等号 不变性（Invariance under transformation） 如果 是单射（可逆）变换，则 意思是：在做变量的可逆变换时，KL 散度值不变 非负性证明 函数 在 上是凸函数，由 Jensen 不等式，对于以 为权的随机变量 （这里 ）有： 同时 因此左边等于 ，于是 所以 。 取等条件：Jensen 取等号当且仅当 几乎处处为常数，即 在 几乎处处为常数，但 ，所以该常数必须为 1，从而 ，所以 不变性证明 若 是可逆（双射）且可测的变换，令 。若 在 上有密度 ，则 在 上的密度分别为 ，并且 假设...

3. 如果,是高斯分布，那么正比于高斯分布 情形1:不同变量与 (独立联合分布) 设 定义： 这个 就是块对角矩阵（block diagonal matrix），因为 和 独立，协方差的交叉项为 0 直接相乘： 注意常数项： 其中 表示块对角矩阵，行列式等于子块行列式的乘积 把两部分二次型加起来： 正好等于： 因为块对角矩阵的逆仍然是块对角形式： 于是： 这正好就是： 也就是说，独立的两个高斯的乘积，等于它们拼成的联合高斯分布 情形2：同一变量 上两份高斯相乘 若 则 其中 首先，关注指数项： 令 则有 代回去得到 与无关的常数 因此 常数 即 新的常数 从而证明了“成比例于高斯” 4. 边缘封闭性：如果是高斯分布，那么也是高斯分布 设联合高斯向量 则边缘分布 使用特征函数进行证明 联合高斯向量 的特征函数为 令,则： 边缘 的特征函数就是把 代入联合特征函数： 这正是均值 、协方差 的高斯分布的特征函数，特征函数唯一确定分布，故 证明：边缘 的特征函数就是把 代入联合特征函数 设随机向量 的联合分布为 ，它的...

高斯分布的线性封闭性 1. 如果是高斯分布, 那么也是高斯分布 设 是一个服从高斯分布的随机向量，其均值为 ，协方差矩阵为 ，则的PDF为： 现在，考虑一个新的随机变量 ，其中 是一个矩阵， 是一个向量，我们要证明 也是一个高斯分布 计算 的均值 根据期望的线性性质，我们计算出 的均值 ： 计算 的协方差矩阵 接下来，计算 的协方差矩阵 ： 是常数矩阵，可以移到期望符号外： 又因为： 证明 的 PDF 形式符合高斯分布 使用特征函数证明线性变换下的高斯分布的特征函数仍然是高斯分布的形式 的特征函数为： 的特征函数为： 令 ，我们可以发现 实际上就是 的特征函数 ： 这个最终形式的特征函数，正是均值为 、协方差矩阵为 的高斯分布的特征函数。因为特征函数唯一地确定了概率分布，所以： 仍然服从高斯分布。 2. 高斯分布的线性组合也是高斯分布 以两个相互独立的高斯随机变量 和 为例进行证明，设 ，目标是证明 也是一个高斯随机变量 一个服从高斯分布 的随机变量，其特征函数为： 利用特征函数的定义来计算 的特征函数 ： 由于 和...

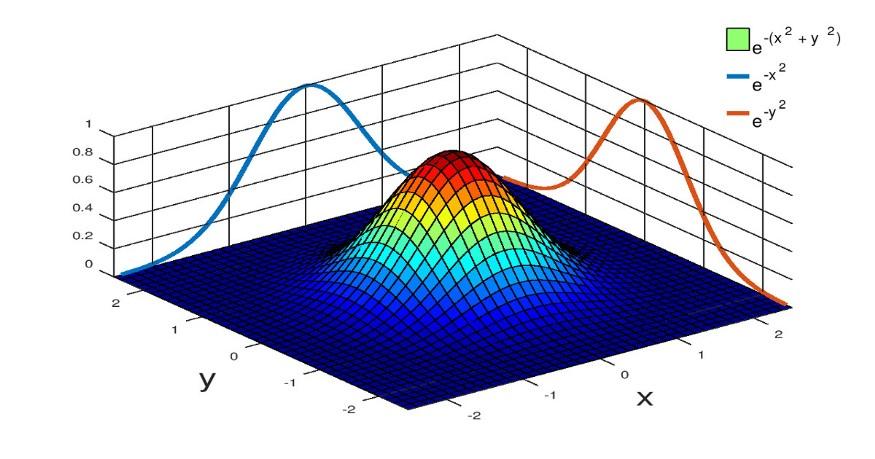
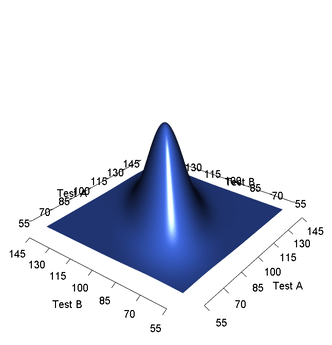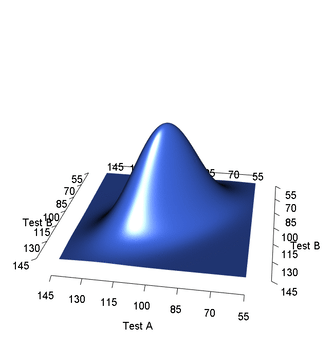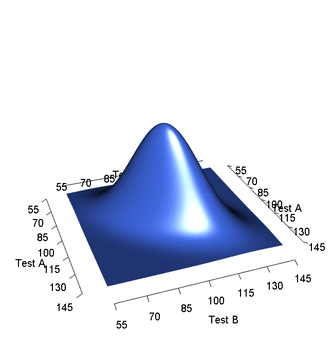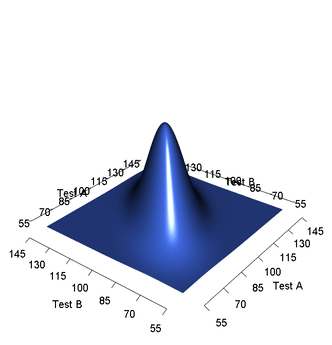
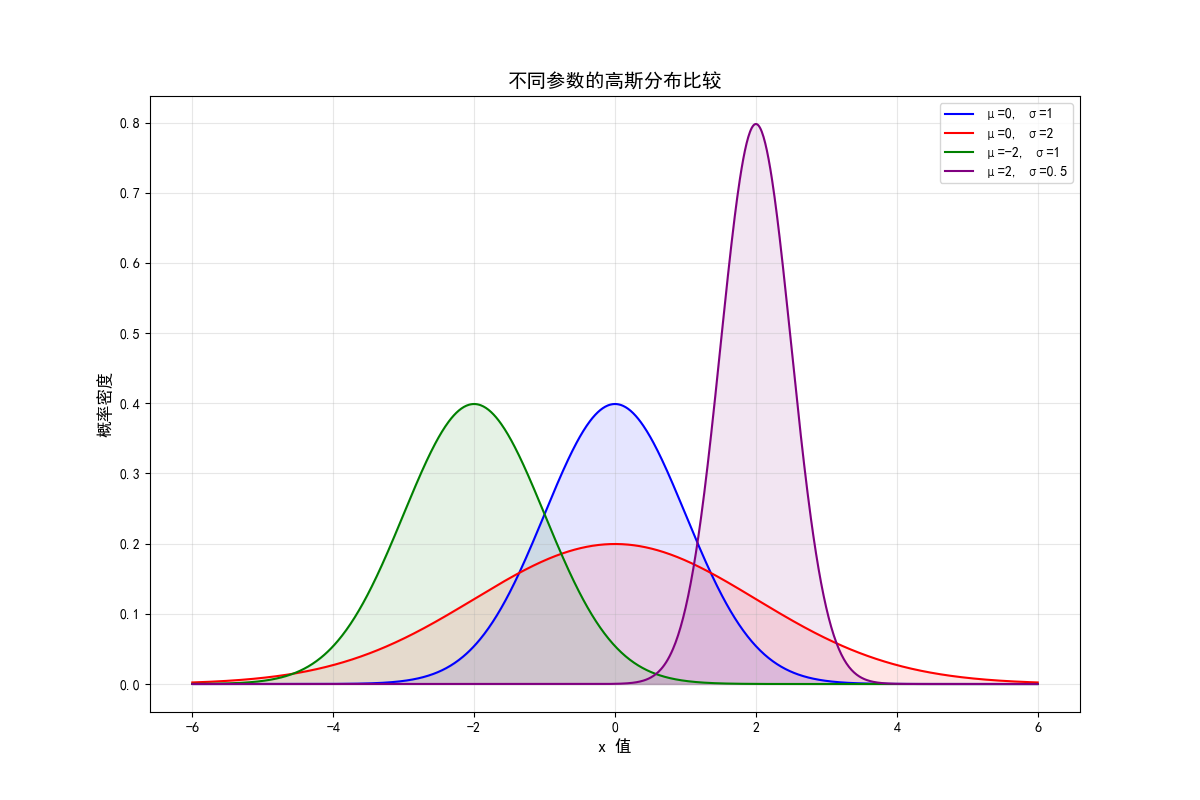
高斯分布 一维高斯分布 一维高斯分布的概率密度函数（PDF）呈钟形： 均值 ：决定了钟形曲线的中心位置 方差 ：决定了钟形曲线的胖瘦程度 公式为： 用符号 来表示随机变量 服从均值为 、方差为 的高斯分布 二维高斯分布 二维高斯分布的形状由以下参数决定： 均值向量 ： 表示分布的中心点在平面上的位置 协方差矩阵 ：描述了两个维度之间的方差和协方差关系 二维高斯分布的概率密度函数公式为： 是一个二维数据点， 是协方差矩阵的行列式。 维高斯分布（多元高斯分布） 多元高斯分布由以下参数决定： 均值向量 ：一个 维向量，表示分布的中心 协方差矩阵 ： 一个 的对称正定矩阵，对角线元素是各维度的方差，非对角线元素是协方差 维高斯分布的概率密度函数公式为： 这里， 是一个 维数据向量 特别地，VAE中出现的都是对角矩阵 高斯分布的特征函数 推导核心：配方法(completing the square) 来求解积分 推导 的特征函数 定义和初始设置 n维高斯分布的 PDF： 特征函数的定义： 积分代入和准备 将 PDF 代入特征函数的定义中： 将...

PDF与特征函数 特征函数和概率密度函数是描述随机变量概率分布的两种重要数学工具，它们之间存在着一种深刻而优美的傅里叶变换对（Fourier Transform Pair）关系 简单来说，PDF 描述的是随机变量在实数域上的行为，而特征函数描述的是随机变量在频域上的行为，它是PDF 的傅里叶变换 对于一个连续型随机变量 ，其概率密度函数为 特征函数 定义为 的期望，即： 这个公式正是傅里叶变换的定义,它把 这个定义在实数域上的函数，变换到了频域上的函数 因为它们是傅里叶变换对，所以我们可以通过傅里叶逆变换，从特征函数反过来得到 PDF： 这个公式表明，只要我们知道了一个随机变量的特征函数，就可以唯一地、精确地还原出它的概率密度函数 为什么说这是一种强大的关系？ 唯一性：这种傅里叶变换对的关系保证了一一对应,这是我们能够利用特征函数来证明分布性质的根本原因 数学运算的简便性：某些在实数域内非常复杂的运算，在频域会变得异常简单 独立随机变量的和：如果 和 是独立的，那么它们的和 的特征函数是它们各自特征函数的乘积：，而在 PDF 域，这需要进行复杂的卷积运算：...

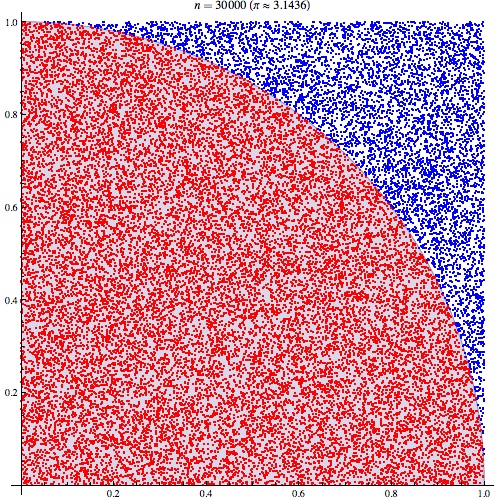
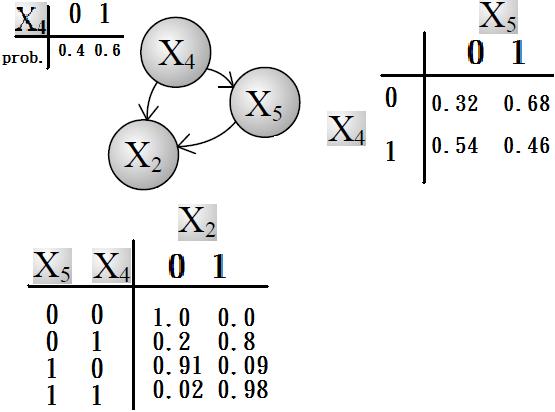
蒙特卡洛方法 核心思想：利用随机抽样逼近期望值 蒙特卡洛方法利用随机抽样来近似计算一个量的期望值，从而解决该量的数值问题，这个量通常是积分 假设我们想要计算一个函数 在某个概率分布 下的期望值 ： 当这个积分很难直接计算时，蒙特卡洛方法提供了一种近似解法 从概率分布 中独立地抽取 个样本点： 利用这些样本点来近似期望值： 被称为蒙特卡洛估计量 大数定律 根据大数定律（Law of Large Numbers），当样本数量 时，样本均值会收敛到期望值： 链式法则 假设我们有两个随机变量 和 ，它们的联合概率 可以表示为： 或者 这两种形式是等价的，根据条件概率的定义 很容易推导出来。 推广 对于多个随机变量 ，它们的联合概率 可以通过链式法则分解为： 更一般的形式是： 特别地，这里的 就是

贝叶斯估计 核心：把参数本身也看作是随机变量 在最大似然估计中，模型参数被认为是一个固定但未知的值，我们通过数据来“猜”出它最可能的值 而在贝叶斯估计中，我们认为参数是一个服从某个概率分布的随机变量,这个概率分布描述了我们对所有可能取值的信念（belief） 过程: 先验信念 + 观测数据 后验信念 这三个关键概念分别对应： 先验分布 (Prior Distribution) ：在看到任何数据之前，我们对参数 的初始信念,反映了我们对参数的先验知识或经验 似然函数 (Likelihood Function) ：和最大似然估计中的似然函数是同一个概念,描述了在给定参数 的情况下，观察到现有数据 的概率。 后验分布 (Posterior Distribution) ：在观察到数据 之后，我们对参数的更新后的信念,结合了先验信念和数据提供的新信息 这三者之间的关系由贝叶斯定理(Bayes’ Theorem)来描述： 其中： ：后验分布 ：似然函数 ：先验分布 ：边缘似然(Marginal Likelihood)，用于对后验分布进行归一化 因此，贝叶斯定理可以简化...

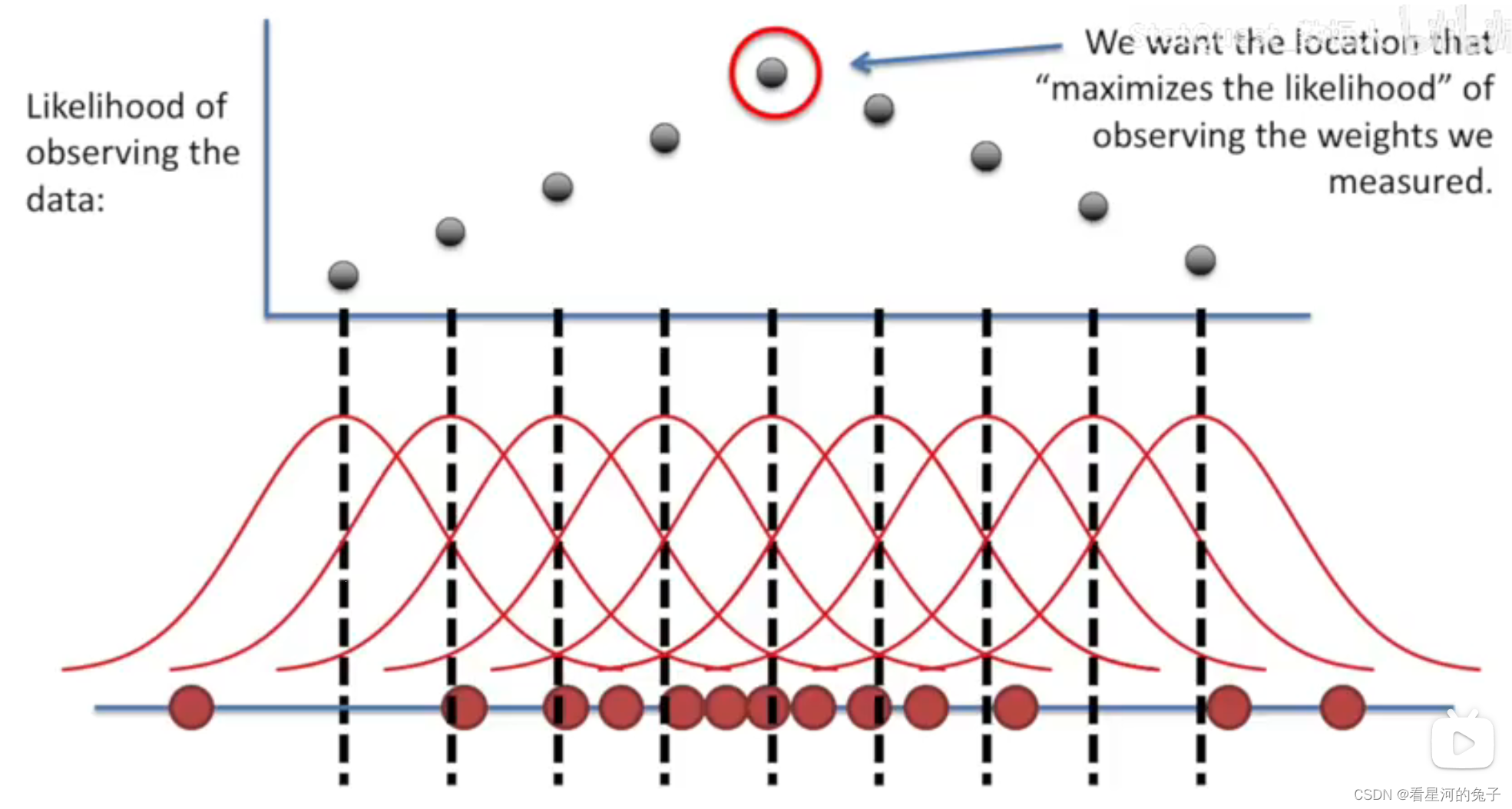
最大似然估计 假设有一个概率模型(这个是前提)，其概率密度函数为 是观测到的数据 是想要估计的模型参数 目标是，找到一组参数值 ，使得观察到现有数据的概率最大 与贝叶斯估计不同的是，我们认为是一个固定但是未知的值 似然函数 存在有一组独立的、同分布（i.i.d.）的观测数据 在给定参数 的条件下，观察到这组数据的联合概率是所有单个观测值概率的乘积： 这个函数 就是似然函数，是一个关于参数 的函数，表示在不同 值下，数据 出现的“可能性”大小 对数似然函数 为了方便计算，对似然函数取自然对数，得到对数似然函数： 由于对数函数是单调递增的，最大化似然函数 等价于最大化对数似然函数 。 最大化与参数估计 最大似然估计量 就是使对数似然函数达到最大值的那个参数 ： 为了找到这个最大值，计算对数似然函数对参数 的偏导数，也称为得分函数（score function）。 令得分函数等于 0， 求解这个方程，得到的解就是最大似然估计量 局限性 数据量较少时，会存在比较严重的过拟合问题