分数视角

参考文献

Papers

Blogs

基本设定

分数生成建模，即从一个由独立同分布（i.i.d.）样本构成的数据集中，学习一个未知数据分布

其中：

分数（Score）：概率密度的分数被定义为，即对数概率密度的梯度场
分数网络（Score Network）：一个由参数化的神经网络，它将被训练来近似的分数，即
生成建模目标： 利用数据集学习一个模型，用以生成来自的新样本

整体框架而言，分数生成模型旨在通过训练一个分数网络来估计数据分布的梯度（分数），然后利用这些梯度配合朗之万动力学来生成新样本

从EBMs的视角看分数函数的优势

对于EBMs来说，

其中，是归一化常数：我们希望：对于这个式子而言，是极难优化的，从而对于也是极难优化的

但是,如果引入分数函数： $与互相独立$

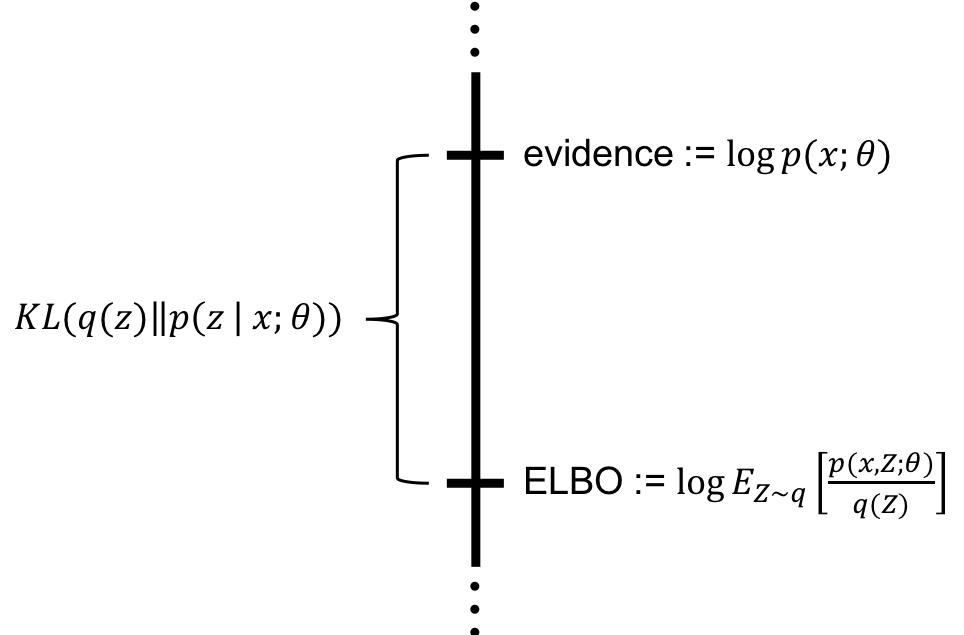
Score-based Model 的优化目标

Fisher Divergence

分数匹配的优化目标：最小化模型分数 与数据分数 之间的差异

Score Matching: 解决的不可计算问题

分部积分化简

仍然包含一个未知量：数据分布的分数

我们接下来通过分部积分的方式来解决这个问题

一维简化推导

对于一维随机变量，费雪散度可以展开为： $假设时，$

多维分数推广

将分部积分推广到多维数据，即分数匹配目标函数：

其中，是关于的雅可比矩阵的迹，即相对于的Hessian矩阵的迹

问题

由于涉及到对于矩阵迹的计算，所以在处于高维数据时，会有很高的计算开销

高维问题解决1: Denoising Score Matching

对于,我们添加一个微扰,得到,那么：其中：不妨设，

对于而言,可以理解为在中采样获得之后加上微扰，上述的表达式可以替换为：

我们对于继续进行计算：

将带回：

定义:

所以说：

那么高维问题就转化为：

其中:

带入原式：

这样可以优化出来,当时，,那么

高维问题解决2: Sliced Score Matching

SSM的核心思想是：与其匹配高维的整个分数向量场，不如匹配它在随机一维方向上的投影

原理： 两个向量场和只有当它们在所有随机方向上的投影都相等时，才证明这两个向量场本身是相等的
优势： 投影将维向量场的匹配问题转换成了标量场的匹配问题，从而避开了计算整个矩阵

所以，我们定义:

这个式子也被称为 Sliced Fisher Divergence

其中，一般被选择为：

标准高斯分布：
球形均匀分布：即是一个维单位球面上均匀采样的方向向量

切片 Fisher 散度仍然不可计算,通过应用分部积分技巧，将其转换为可计算的切片分数匹配目标函数：

展开：

下面展示如何快速的计算:

第一次梯度操作：计算分数函数
第二次梯度操作：计算，即，然后将结果与做点积

由于的计算对所有个都是共享的，因此总共只需要次分数函数计算 + 次二次型计算，总共次梯度操作

与原始 SM 的对比

假设的维度是，且，通常需要次梯度操作来计算，因为的每个对角线元素都需要单独计算

朗之万动力学与朗之万采样

我们已经通过上述的score matching方法,成功学习到了分数场，下面需要借助分数场进行生成

朗之万动力学

朗之万动力学是一种MCMC采样算法，可以在不知道完整概率密度函数本身，只知道其分数函数的情况下，从分布中生成样本

$分数项漂移项噪声项扩散项$

步长 (): 控制每一步的移动距离和噪声强度
分数项 ()：根据分数函数（梯度），将样本推向概率更高的区域
噪声项 ()： 随机热噪声（布朗运动），确保算法能够探索整个分布空间，避免卡在局部最优解

收敛性

理论上，要求步长趋近于零，迭代次数趋近于无穷大，MCMC过程可以完全收敛到目标分布

朗之万采样

我们已经训练了一个模型来近似真实的分数函数，我们就可以用这个模型替代真实分数函数：

其中，可以从任意分布中进行采样

通过这个过程，利用训练好的神经网络模型进行迭代，从而生成类似于真实数据的样本

Naive Score-based Generative Modeling的问题

流形假设

真实世界中的数据（例如，图像、文本、语音等）虽然存在于一个高维空间（ambient space，例如一张的彩色图片对应维空间），但它们实际上只集中在这个高维空间中一个或几个低维子空间上，这些子空间被称为低维流形（low-dimensional manifold）

这个假设意味着我们只需要学习和理解数据在这个低维流形上的结构和变化，而不是整个高维环境空间

Score-based Generative Modeling在流形上的两大困难

困难一: Undefined Score Function

如果数据严格限制在一个低维流形上，这意味着流形外部的概率密度几乎为零,在数学上，如果的支撑集是一个低维流形，那么它在环境空间中通常不能被表示为一个连续的概率密度函数,在这种情况下，对数概率密度在环境空间中不可微，分数是未定义的

困难二：Inconsistent Score Function

原始的分数匹配理论要求数据分布的支撑集必须是整个高维环境空间,只有在这种情况下，最小化分数匹配目标才能保证训练出的一致地估计出真实的分数

在支撑集不覆盖整个空间时，原始的分数匹配目标函数将是不一致的,即使神经网络具有无限容量，并且我们完美地最小化了目标函数，训练出的仍然不能保证是真实分数函数的良好估计

表现: Low data density regions (低维流形之外)

Inaccurate Score Estimation with Score Matching

训练出来的分数估计函数在低密度区域（即数据点稀疏的区域）非常不准确，因为低密度区域的真实数据点很少

由费雪散度：

在高密度区域，很大，模型会确保这些区域的误差最小；在低密度区域，接近于零，整个误差项（差异权重）对总损失的贡献极小

因此，训练过程倾向于忽略低密度区域的分数准确性

Slow Mixing of Langevin Dynamics

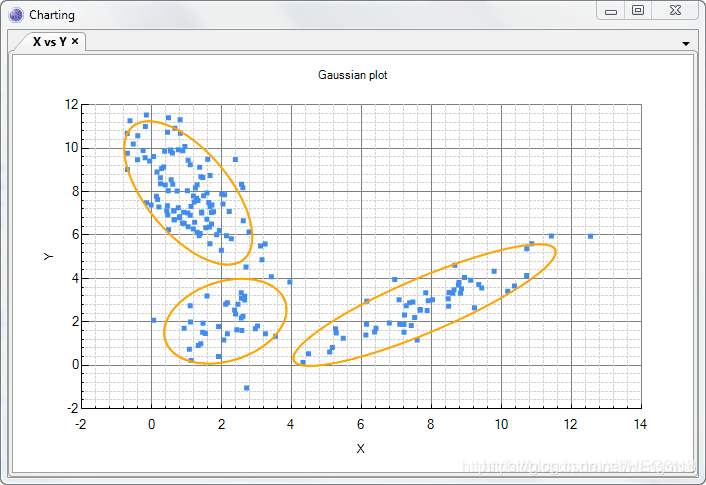
当数据分布是多峰的（混合高斯分布），且不同“峰”之间被数据稀疏的低密度区域分隔开时，朗之万动力学无法在合理的时间内在这些模式之间高效地跳转，即混合

如果 MCMC 链无法充分混合，就无法正确地遍历整个分布空间，导致最终的样本集不能准确反映各个模式的真实相对权重

数学分析局限性

这种缺陷是分数函数本身的性质导致的

假设目标分布是两个分布和的混合，且它们的支撑集是不相交的

模式 1 (在区域)的分数:

模式 2(在区域)的分数:

在两个分离的模式内，分数函数仅取决于模式本身的形状 ( 或 )，而与它们之间的相对权重无关

朗之万动力学仅依赖分数函数进行采样，因此，如果朗之万链随机初始化在一个模式内，它会有效地沿着该模式的梯度移动，但无法感知到该模式应该占据多大的比例 ()

理论上，朗之万动力学仍然可以混合，但需要极小的步长和极大的步数才能在低密度“山谷”中成功跳跃

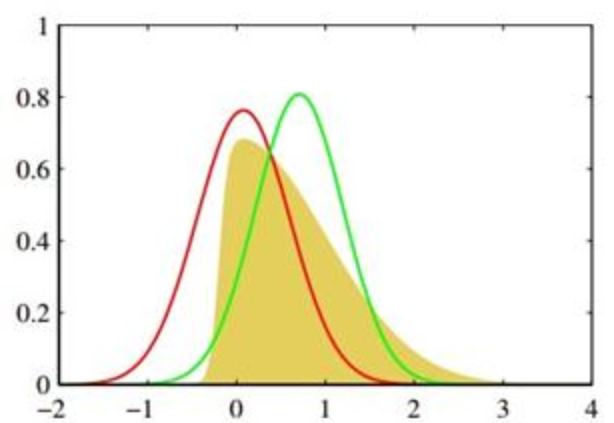
图 3(a) 是精确采样（反映了真实的权重）
图 3(b) 是朗之万动力学采样,如图所示，朗之万动力学采样的样本在两个模式之间的相对密度是错误的
图 3(c) 展示了使用退火朗之万动力学 采样的结果,能够恢复两个模式之间的相对权重

Noise Conditional Score Networks (NCSN)

模型采用了同时使用多尺度噪声扰动的方法

使用个递增的标准差

Noise-Perturbed Distribution: 对于每个噪声，原始数据分布被扰动，得到噪声扰动分布
NCSN: 训练一个噪声条件评分模型 (Noise Conditional Score Network, NCSN) 来估计每个噪声扰动分布的评分函数，使其近似满足：

训练目标

对于任意给定的噪声而言：

且：那么训练目标变为：

那么对于所有的而言：

是一个正权重函数，通常选择为
该目标函数可以通过评分匹配方法进行优化

推理：Annealed Langevin Dynamics

在训练完噪声条件得分模型后，可以通过运行朗之万动力学次序列来从中生成样本。这种方法被称为退火朗之万动力学，因为噪声尺度随着时间逐渐减少 (退火)

几点实用建议：

选择作为一个项的等比数列，其中足够小，而应与相当
使用U-Net skip connections对得分模型进行参数化
在测试时使用得分模型时，对其权重应用指数移动平均