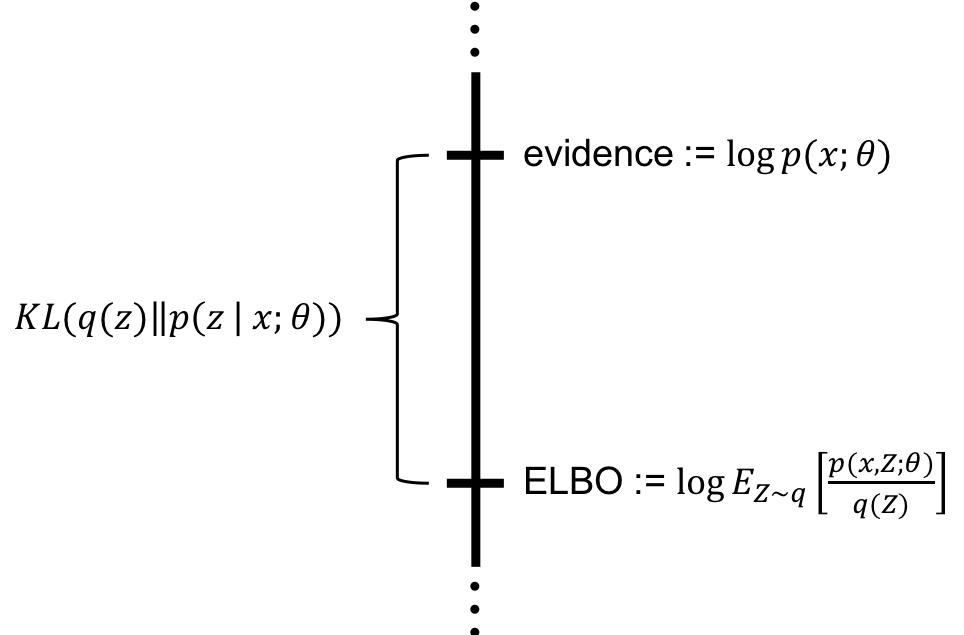
Diffusion2-能量视角
能量视角
参考文献
Papers
Blogs
从能量视角下的GAN开始
能量模型 (EBM) 的定义
能量模型
最大似然估计的梯度推导
训练 EBM 的目标:最大化训练数据的对数似然
现在,我们对参数
用生成器
基于能量模型
所以训练目标变为:
其中:
生成器
为了让
对于
对于上述公式,我们发现,由于
有关熵问题的处理
我们尝试通过显式的方式对此进行一定程度的分解:
由:
容易得到:
但在连续空间中,
同时定义互信息
所以说,互信息可以分解为边际熵
条件熵定义为:
计算
离散情况下,
连续情况下,考虑
当
因此在这个问题中,可以把
我们一般认为近似后验是一个高斯分布
所以:
所以说:
同时我们需要确保在
MCMC方法与郎之万方程
MCMC 的基本概念
MCMC,马尔科夫链蒙特卡洛方法(Markov Chain Monte
Carlo),当难以直接从目标分布
核心思想是:构造一个特殊的随机过程,使得该随机过程的静态分布是目标分布
其中
从任意
Langevin 方程:MCMC 的一个特例
Langevin方程:
当
其中
直接对高维数据
转移到对隐变量
隐变量
对
优势:
- 维度问题解决:
- 噪声问题解决: