Diffusion的数学推导与具体实现

参考文献

1.DPM

Diffusion的前向过程(Forward Process)

前向过程是一个固定的马尔可夫链，它逐步向数据中添加高斯噪声，直至数据完全变成纯噪声,即代表的过程

用数学公式表示如下：

其中，是真实数据样本，是在每个时间步添加的噪声方差，构成一个固定的方差调度表

前向过程的关键特性

通过重参数化，可以在任意时间步闭式地得到的采样，而无需逐步迭代

定义和

则对上文公式进行重参数化有：代入的表达式: 继续代入到: 然后根据高斯分布的封闭性以及推导公式，最终高斯分布参数为: 最终可以得到一个简洁的闭式形式：

这个公式是训练阶段的核心，它可以直接从原始数据采样出任意时间步的加噪样本

Diffusion的反向过程(Reverse Process)

反向过程是一个由模型学习的马尔可夫链，从纯噪声开始，逐步去噪，直到生成一个真实的数据样本

这个过程的每一步都是一个由神经网络参数化的条件高斯分布：

其中，和是需要学习的参数，通常由一个神经网络(如U-Net)来表示

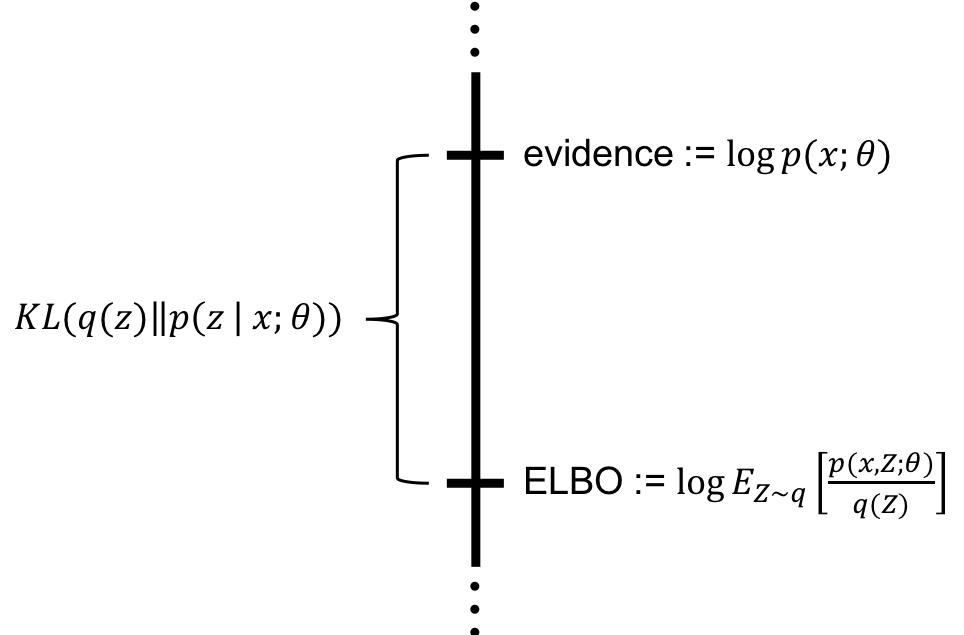
训练目标与ELBO

在潜在变量模型（如变分自编码器VAE和扩散模型）中，我们通常无法直接计算数据的对数似然，因为需要对所有可能的潜在变量（在这里是整个路径）进行积分 ELBO 是对这个无法计算的对数似然的给出一个可计算的下界，我们通过引入一个近似后验分布来得到它，根据变分推理的原理，我们有：其中，

是联合分布，表示模型中的前向和反向过程
是前向过程的联合概率分布

形态1:

：这是由模型的反向过程定义的从到的路径上的概率，它代表了模型从噪声生成数据的过程
：这是由DDPM中固定的前向过程定义的从到的路径上的概率

形态2:

展开联合分布推导可得：

整个扩散过程（包括前向和反向）是一个马尔可夫链(系统的下一个状态只依赖于当前状态，与过去的历史状态无关)

对联合概率应用链式法则：
模型假设反向过程是一个马尔可夫链。这意味着，在第步去噪得到时，也只依赖于当前状态，与更远的未来状态无关 $即：$
对于前向过程而言，也是一个马尔可夫过程

将它们代入ELBO的定义，然后使用对数和的性质：

这个式子中的每个项都有其物理意义：

：是一个常数项，因为是一个标准正态分布，与模型参数无关，实际训练可以忽略这个项

形态3:

由形态2:

此处应选用同一变量的分布，所以利用贝叶斯公式进行转换

形态3.1 引入进行转换,我们认为约等于

形态3.2 直接转换

$我们认为约等于约等于$

有关训练

与VAE相同，训练的目标是最大化ELBO

因为我们在训练中会选择更为贴近工程实际的形态3.1，即：

其中，是前向过程的后验分布，它是一个可求闭式解的高斯分布

计算后验

首先通过贝叶斯公式将后验概率转化为先验概率：

此时不影响的分布，只是作为一个归一化常数出现;同时又因为马尔可夫过程，,所以：

其中，

两个高斯分布和的乘积仍然是一个高斯分布，其参数为：

使用该公式本身就能够保证归一化问题

之后，我们要对进行乘积计算： $视为关于的函数正常计算$

计算

显然：

对于, 展开原式得:

我们将其重新整理为关于的函数：

忽略所有不含的项（如），因为它们是关于的常数：

将上式与标准高斯分布的指数部分进行比较

在标准高斯形式中，二次项是 ,在我们的表达式中，二次项是
在标准高斯形式中，一次项是 ,在我们的表达式中，一次项是

因此，即：

计算后验协方差()

令：

利用恒等式和：

代入：

那么就有：

计算后验均值

带入公式：

那么：

即对于：

对其中的每一个KL散度而言，都可以通过计算过程的闭式解从而使用Rao-Blackwellized方法求解而不是通过有显著方差的Monte Carlo方法求解

2.DDPM:Diffusion Models and Denoising Autoencoders

新的训练目标与参数设定

前向过程与模型设计

决定前向过程的被固定为常数，也即：

前向过程中没有可学习参数
变为常数，可以忽略

反向过程与模型设计

反向过程定义为高斯分布：

协方差的选择

协方差矩阵设置为固定、与时间相关的对角矩阵：

两种极端的固定选择和在实验结果上相似

：对应于原始数据时的最优选择
：对应于是一个确定点时的最优选择
这两种选择分别对应于逆向过程熵的上下界

均值的参数化选择及其理论推导

当逆向过程的协方差固定为时，由公式：

可以将项中的KL散度展开为一个均方误差项加上一个与无关的常数：

$常量$

其中是前向过程的真实后验均值，可以解析
所以，优化最直接的方法是让模型去预测真实的后验均值

为了简化目标，引入了重参数化技巧：

将此带入真实后验均值的展开式中：

将这个展开式代入的均值项：

$等价于$

为了最小化损失，必须预测

-预测的参数化

基于上述公式，一种特定的参数化 被提出，让模型去预测噪声：

模型不再直接预测均值，而是从预测噪声，然后用间接计算均值

将参数化后的带入loss：

优化复杂的ELBO的项，等价于优化一个简单的、加权的MSE Loss，该Loss要求模型预测真实噪声

这个目标函数形似去噪得分匹配(Denoising Score Matching)

新的 -预测参数化直接简化了采样过程：

同时也自然提出了训练目标的简单形式:

训练过程

从真实数据分布中采样一张原始数据
从 $中$ 均匀地采样一个时间步长
从标准正态分布中采样一个纯噪声向量
：执行一次梯度下降，最小化关于和预测的 MSE 损失
重复直至收敛

采样过程

训练完成后，通过逆向过程从噪声生成图像

从标准正态分布中采样纯噪声图像
循环进行以下步骤：
- 使用训练好的网络预测当前噪声水平下的噪声
- 计算去噪后的样本：其中，通常设置为常数，例如或
最终得到生成的图像