VAE的应用以及理论依据

训练后的两种应用

1. 直接生成 (Direct Generation)

  • 如何操作？
    • 此时可以抛弃 encoder
    • 从一个先验分布 （通常是标准正态分布）中采样 Z
    • 通过解码器（decoder）做一个映射 ，也就是生成图像
  • 为什么可以这样做？
    • 因为在 VAE 模型的优化过程中，encoder 的近似后验分布 和先验分布 已经被拉得比较接近

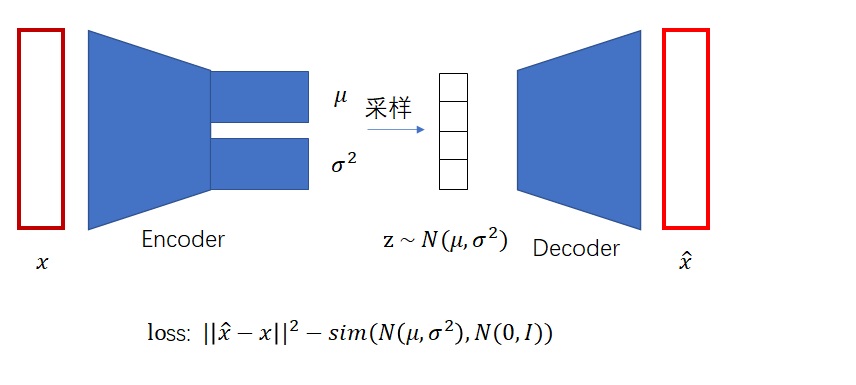
2. 重构原来的图像 (Reconstruction)

  • 如何操作？
    • 此时需要同时使用 encoder 和 decoder
    • 首先，基于 encoder ，对输入图像 X 进行编码，得到潜在表示 Z
    • 然后，基于 decoder ，利用得到的潜在表示 Z，生成重构图像
  • 目的？
    • 验证 VAE 是否能够学习到对数据的有效压缩和解压表示
    • 确保模型能够将输入数据映射到潜在空间，然后再从这个潜在空间中准确地恢复出原始数据，这通常是评估 VAE 训练效果的一个重要指标

理论依据

高斯分布+CDF逆变换拟合任意分布

  • 假设：

    • 随机变量 服从标准正态分布
    • 它的CDF（累积分布函数）记为

  • 第一步：高斯分布到均匀分布

    • 如果 ，那么将其CDF应用于自身，得到的随机变量 将服从均匀分布
    • 证明：
      • 我们想求 的CDF，即
      • 因为 是单调递增的，所以可以取逆函数
      • 根据定义，右侧的表达式就是 的CDF在点 处的取值，即
      • 所以 的CDF是 。这正是均匀分布 的CDF

  • 第二步：均匀分布到目标分布

    • 假设：
      • 随机变量 服从均匀分布
      • 目标随机变量 对应的CDF是
    • 结论：
      • 随机变量 服从分布
    • 证明：
      • 我们想求 的CDF，即
      • 因为 是单调递增的，所以可以取正变换
      • 因为 是均匀分布在 上的，所以
      • 将 代入，得到
      • 所以 的CDF是 ，这证明了 服从目标分布

因此，我们可以通过“高斯分布 -> 均匀分布 -> 目标分布”的两步变换过程，从高斯分布生成任何我们想要的分布的随机数