VAE的前向过程及核心代码

VAE的前向过程及核心代码

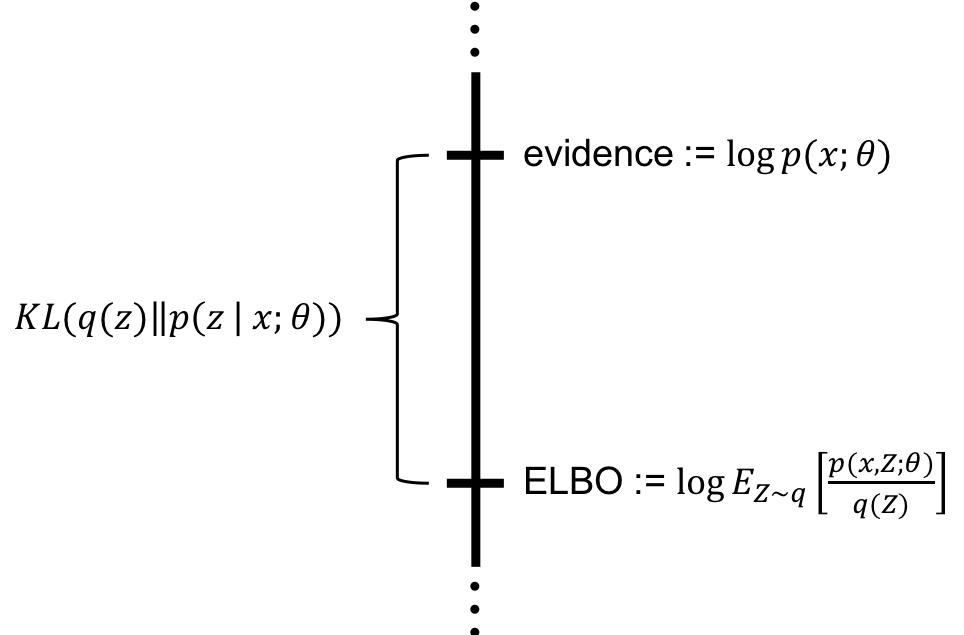
ELBO 目标函数：

代入建模：

对 求导的思路

对 求导是相对简单的因为 只存在于第一项的对数似然项中，可以常规地进行梯度下降

对 求导的思路

第一项（重建损失）：

由于期望的分布本身依赖于参数 ，直接求导无法进行反向传播,因此，需要使用 “重参数化（reparameterization）” 技巧来解决

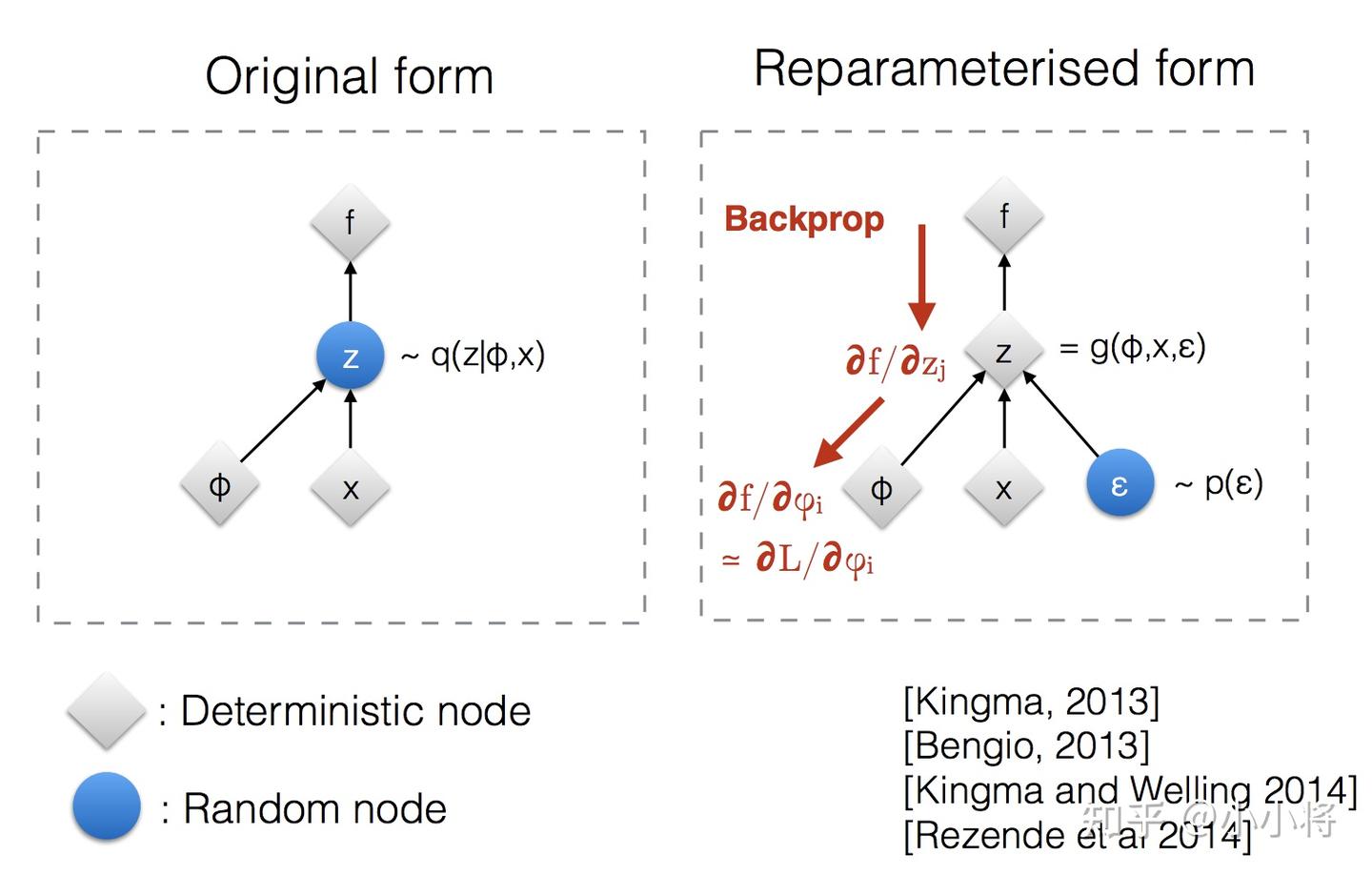
• “变换之前”：我们从一个由 参数化的分布中直接采样潜在变量 ，即 ，这个过程不可导
• “变换之后”：我们引入，通常从标准正态分布中采样，即 。然后，将 转换为潜在变量 ：
• 求导问题：通过重参数化，原来的期望 就变成了对 的期望
• 可以将梯度符号 “穿过” 期望符号 ，

第二项（KL 散度）：

这一项可以进行显式计算，即当 和 都为高斯分布时，KL 散度有一个解析解

计算思路

最后计算的式子为：

应用蒙特卡洛（Monte Carlo, MC）方法：

• 从标准正态分布 中，采样出若干个随机变量
• 利用采样得到的 ，通过重参数化公式 计算得到潜在变量
• 计算近似 ELBO：
• 通过反向传播对 和 求导，并使用梯度下降法来更新编码器和解码器的参数

前向过程

1. 输入数据 (Input Data)

   • 将一个原始数据样本 输入到模型中

2. 编码器（Encoder）

   • 编码器网络将 作为输入
   • 输出：潜在分布（Latent Distribution）的参数 和

3. 重参数化采样（Reparameterization Trick）

   • 从一个标准正态分布 中采样一个随机变量
   • 计算得到潜在变量 ：

4. 解码器（Decoder）

   • 将采样得到的潜在变量 作为输入
   • 输出：重建后的数据
   • 即

5. 计算损失（Calculate Loss）

   • a. 重建损失（Reconstruction Loss）：

     • 衡量原始输入 和重建输出 之间的差异
     • 通常使用二元交叉熵（BCE）或均方误差（MSE）
     • 对应于 ELBO 的第一项：

   • b. KL 散度损失（KL Divergence Loss）：

     • 衡量编码器输出的潜在分布 与我们预设的先验分布 之间的差异
     • 使用解析公式直接计算，无需采样
     • 对应于 ELBO 的第二项：

6. 最终损失（Total Loss）

   • 将重建损失和 KL 散度损失相加，得到用于优化的最终损失值

代码

class VAE(nn.Module):
    def __init__(self, input_dim, h_dim, z_dim):
        super(VAE, self).__init__()
        # === 1. 编码器（Encoder）部分 ===
        # 编码器将输入数据映射到潜在空间的均值(mu)和对数方差(log_var)
        self.encoder = nn.Sequential(
            nn.Linear(input_dim, h_dim),
            nn.ReLU(),
            nn.Linear(h_dim, h_dim),
            nn.ReLU()
        )
        self.fc_mu = nn.Linear(h_dim, z_dim)      # 输出均值 mu
        self.fc_log_var = nn.Linear(h_dim, z_dim) # 输出对数方差 log_var

        # === 3. 解码器（Decoder）部分 ===
        # 解码器将潜在变量Z映射回原始数据维度
        self.decoder = nn.Sequential(
            nn.Linear(z_dim, h_dim),
            nn.ReLU(),
            nn.Linear(h_dim, h_dim),
            nn.ReLU(),
            nn.Linear(h_dim, input_dim),
            nn.Sigmoid()
        )

    def reparameterize(self, mu, log_var):
        # 计算标准差 sigma
        std = torch.exp(0.5 * log_var)
        # 从标准正态分布N(0, 1)中采样一个随机变量 epsilon
        epsilon = torch.randn_like(std)
        # 得到潜在变量 Z
        z = mu + std * epsilon
        return z

    def forward(self, x):
        # 编码过程：通过编码器得到mu和log_var
        h = self.encoder(x)
        mu = self.fc_mu(h)
        log_var = self.fc_log_var(h)

        # 重参数化：得到潜在变量Z
        z = self.reparameterize(mu, log_var)

        # 解码过程：通过解码器从Z得到重建结果
        reconstructed_x = self.decoder(z)

        return reconstructed_x, mu, log_var

# === 4. 损失函数计算（Loss Function Calculation） ===
def vae_loss_function(reconstructed_x, x, mu, log_var):
    # === a. 重建损失（Reconstruction Loss） ===
    # 使用二元交叉熵来衡量输入和重建结果的差异
    BCE_loss = F.binary_cross_entropy(reconstructed_x, x, reduction='sum')

    # === b. KL 散度损失（KL Divergence Loss） ===
    # 使用解析公式计算
    KL_divergence_loss = -0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())

    # === 5. 最终总损失（Total Loss） ===
    # 将两种损失相加
    total_loss = BCE_loss + KL_divergence_loss
    return total_loss, BCE_loss, KL_divergence_loss


def train(input_dim, x):
    # 实例化 VAE 
    vae_model = VAE(input_dim=input_dim, h_dim=256, z_dim=20)
    # 执行前向传播
    reconstructed_x, mu, log_var = vae_model(x)

    # 计算总损失和两种子损失
    total_loss, bce, kld = vae_loss_function(reconstructed_x, x, mu, log_var)

    optimizer.zero_grad()
    total_loss.backward()
    optimizer.step()