隐变量与隐空间
隐变量与隐空间
- 隐变量就是那些我们无法直接观测,但会影响观测数据的变量。
- 它们存在于模型里,用来解释或生成观测到的数据。
用一句话总结:观测不到,但背后起作用的“隐藏因素”
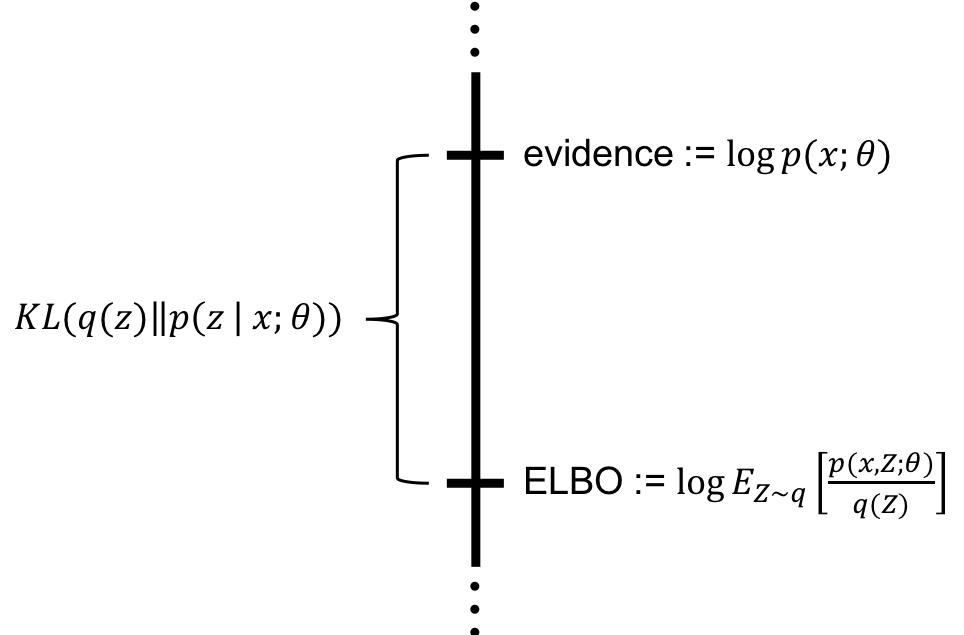
数学表达
在概率模型里:
- 观测变量:
(我们能看到的数据,比如图片、文本、声音)。 - 隐变量:
(不能直接看到的结构,比如图片里的语义标签、风格因子)。
联合分布写成:
如果我们只关心观测数据
对于隐变量的一些基本假设
在含有隐变量的概率模型中,一个完整的数据点不只是观测到的
,还包括生成它的隐变量 ,即一个完整的数据点是 每个样本
对应一个隐变量 ,即对于观测到的数据 ,在生成模型里都假设有某个潜在的 在起作用 我们只能观测到
, 是观测不到的, 通常是数据(比如图片像素), 是抽象的潜在因子(比如姿态、表情、光照) 因为对
积分 往往不可解,直接去优化 是困难的 所以使用分解:
,即观测数据 的分布由“给定隐变量的条件分布”与“隐变量的先验”相乘后积分(求和)得到 一旦
知道了, 或者 是容易优化的
生成模型中的隐变量
隐变量
在生成模型里起决定性作用。 表示“从隐变量到观测数据”的生成过程,即先有 (潜在因素),再产生 (观测结果) 表示了图像中至关重要的本质特征 知道了
,整个图像就可以基于 decode 构建出来,可以理解为 就是 decoder 所要建模逼近的目标 我们会把
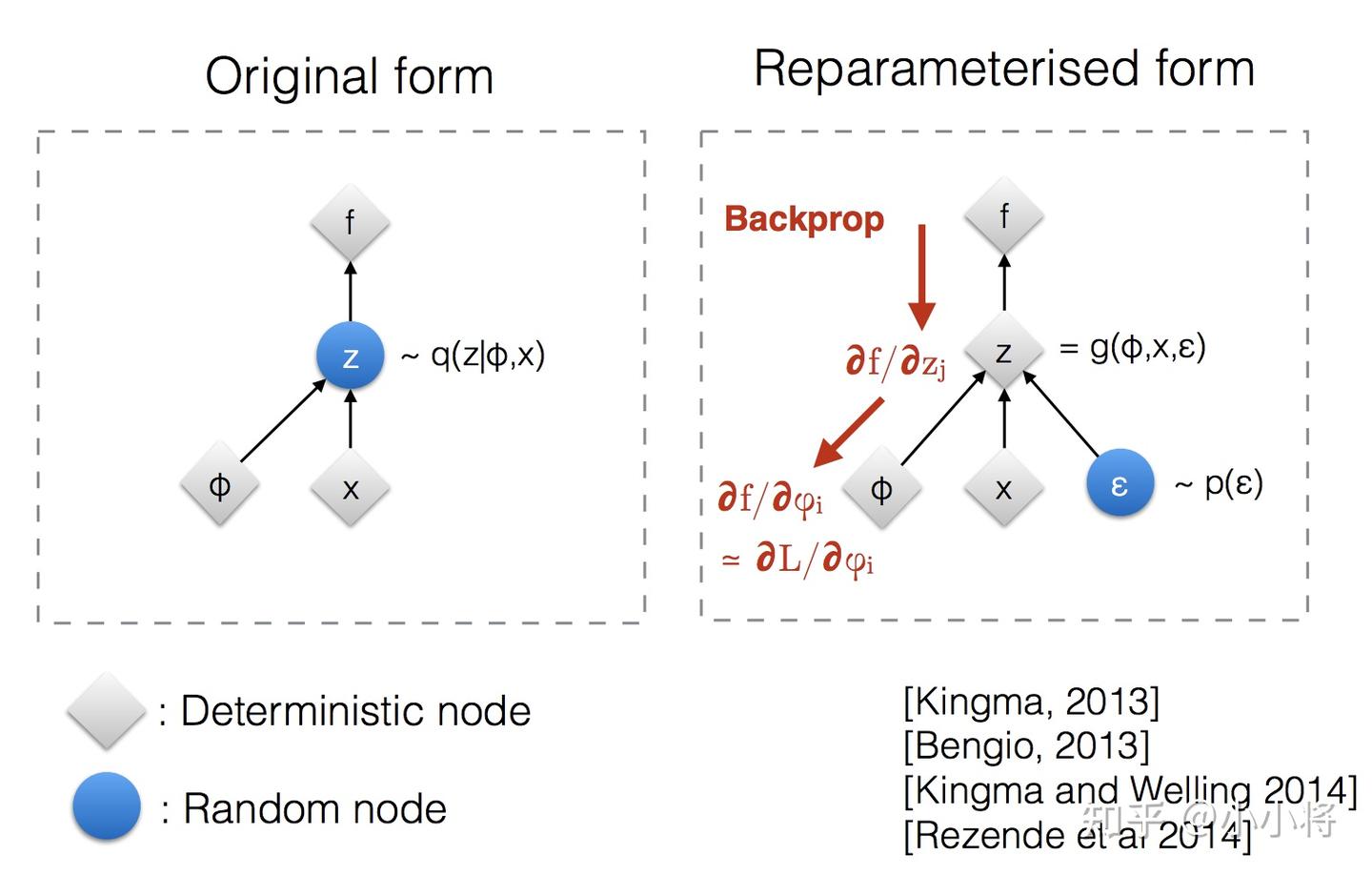
当做是 对一个 encoding 向量,即在 VAE 里,encoder把输入图片 映射到隐变量 ,相当于提取了抽象的“编码表示”。 生成过程:观测值是基于隐变量的值来生成的:从先验分布
中采样一个隐变量,再基于 sample 得到 :根据条件分布生成具体的观测样本。根据 ,说明观测数据的生成过程分为两步:先有隐变量,再生成数据
高斯混合分布
高斯混合分布是一种概率模型,它将一个复杂的数据分布看作是多个简单高斯分布的叠加。
- P(X):我们观察到的数据点的整体概率分布
- P(Z):一个“先验”概率,决定了一个数据点属于哪一个高斯分量(“聚类”)
- P(X|Z):这是“条件概率”,描述了如果一个数据点属于某个特定的高斯分量,它的概率分布是怎样的,在GMM中,这个分布就是一个由自己的均值
(
) 和协方差 ( ) 定义的高斯分布
采样过程
如何从一个GMM中生成一个新数据点:
第一步,先根据先验概率P(Z)决定在哪个群落落点:假设有K个高斯分量,每个分量都有一个权重(
第二步,再根据局部的似然P(X|Z)采样:选择了某个分量后(比如第k个),就从这个分量所对应的高斯分布中随机生成一个数据点,这个高斯分布由它自己的均值
GMM的概率表示与优化
对GMM的参数进行优化,即找到最佳的
直接优化
非常困难 - 总的概率
是所有高斯分量的加权和: 。对这个和取对数 ( ) 在数学上处理起来很复杂,梯度计算也很麻烦,因此直接优化非常困难
- 总的概率
引入“隐变量”Z
- 为了简化问题,我们引入一个隐变量(latent variable)Z。Z是一个one-hot向量,它用来表示每个数据点到底属于哪个高斯分量。例如,如果一个数据点属于第二个分量,Z就表示为 (0, 1, 0, …, 0)
利用联合概率
来解决问题 - 我们不直接优化
,而是考虑联合概率 ,即数据点X和它所属的分量Z同时出现的概率 - 因为Z是one-hot向量,这个公式其实非常简洁:它只会挑出Z所指向的那个高斯分量。例如,如果
,那么公式就等于
- 我们不直接优化
对联合概率取对数,优化变得容易
- 这个表达式同样因为Z的one-hot特性而变得简单。它把原本对一个“和”取对数的复杂形式,变成了对数之和
- 这种形式的表达式更容易进行优化
VAE和GMM之间的联系
VAE是一个特殊高斯混合模型
假设
:定义了 VAE 的先验分布(prior),我们假设潜在变量 服从标准正态分布。这就像 GMM 中每个高斯分量都有一个权重 ,但 VAE 中这个先验分布是连续的 假设
: - 这定义了 VAE 的解码器,表明给定一个潜在变量
,我们生成的观测数据 服从一个高斯分布。关键在于: 这个高斯分布的均值 和协方差 不是固定的,而是由一个神经网络(解码器)根据输入的 计算出来的。这意味着,不同的 会产生不同的高斯分布
- 这定义了 VAE 的解码器,表明给定一个潜在变量
: - 在 GMM 中,由于
是离散的,这个积分变成了求和: - 在 VAE 中,由于
是连续的,我们必须使用积分
- 在 GMM 中,由于
因此,VAE 是无数个高斯的混合