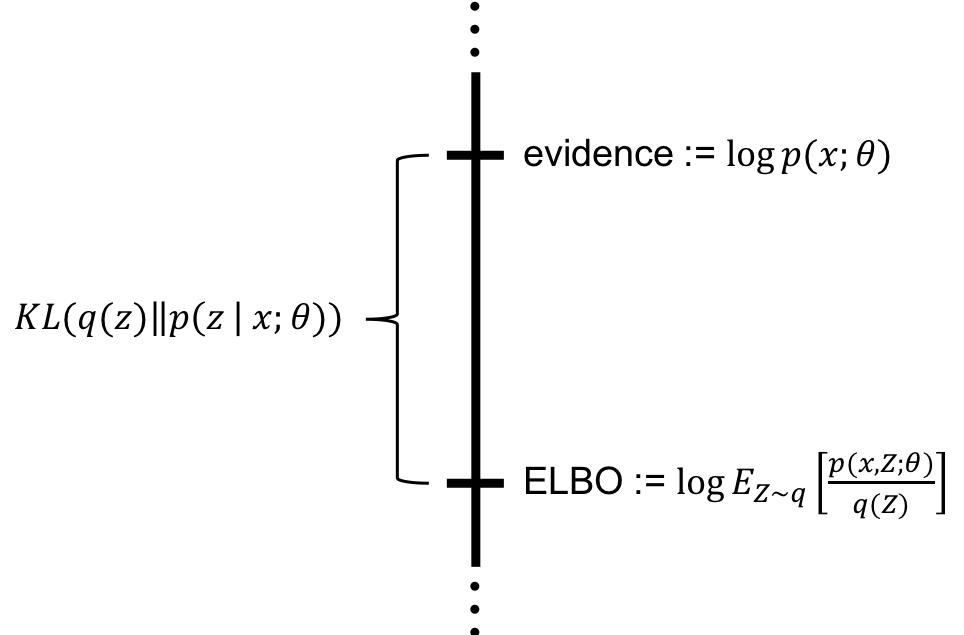
重参数化

PDF中不含参数求函数期望的梯度

由期望的积分定义：

可以将求导号移入积分：

这个形式下可以直接使用蒙特卡罗方法进行求解

PDF中含参数求函数期望的梯度

如何解决的计算成为了一个问题

解决方法一： log trick

定义 且对 可微。令

对两边关于 求导（链式法则）：

移项得到

由上述恒等式代入

即

这就是打分函数 score function形式

这个方法具有通用性，但问题是方差很大

解决方法二： 重参数化

常见的目标形式是：

但直接对这个期望求梯度比较麻烦，因为 的分布 依赖于

重参数化的核心思想是把依赖 的随机性转移到一个固定分布的随机变量 上，从而“分离”随机性与参数

即：

与无关

于是期望可以写成：

  • 先证明:

证明完毕后将上述结果代入：

对 求梯度时， 的分布不依赖 ，所以：

这时我们可以 直接对被积函数求导再采样估计，避免了方差巨大的 score function

特点：方差小，但是并不通用