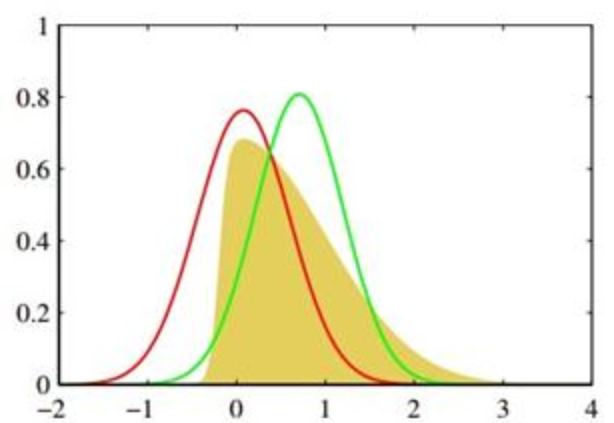
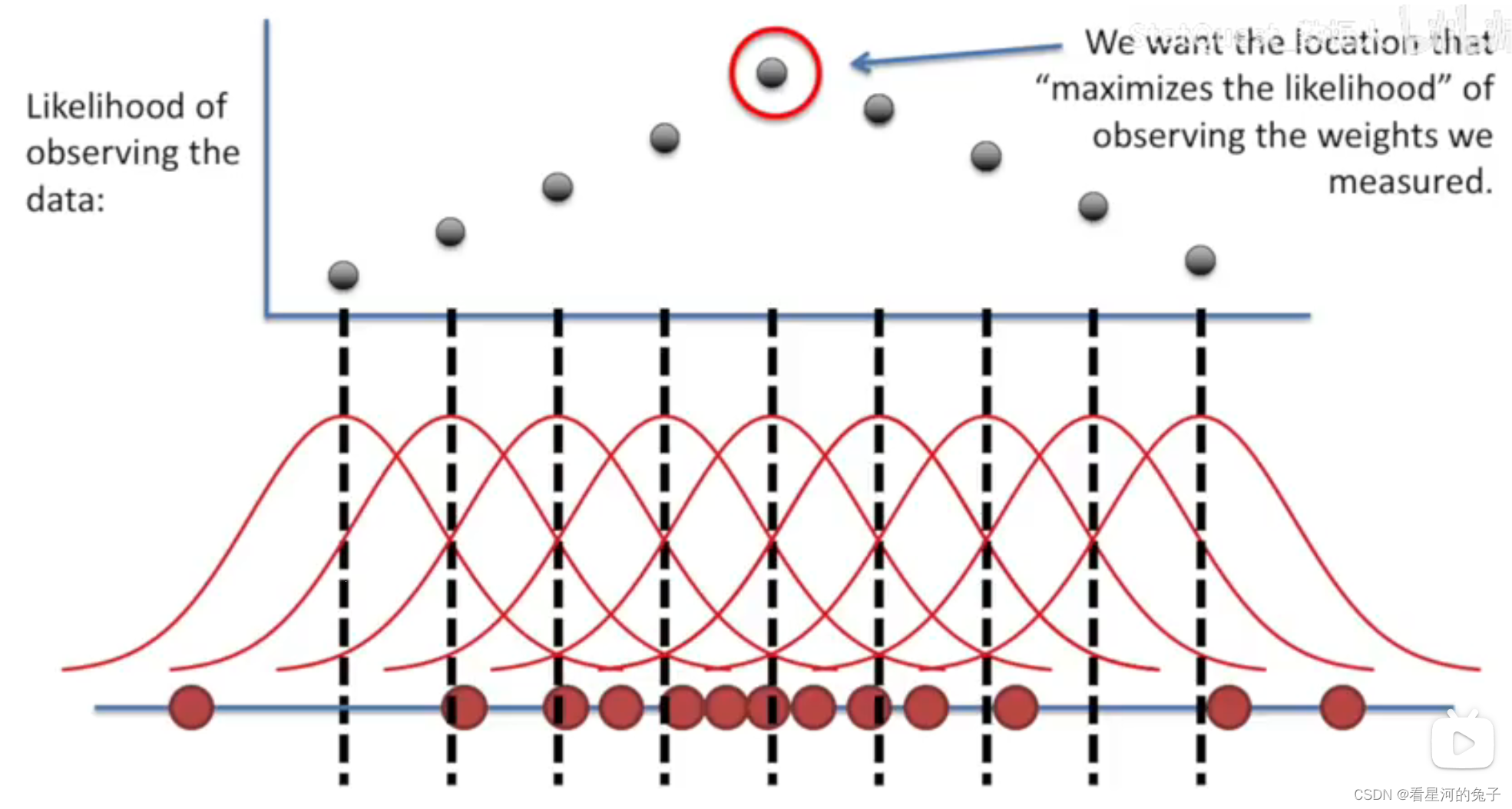
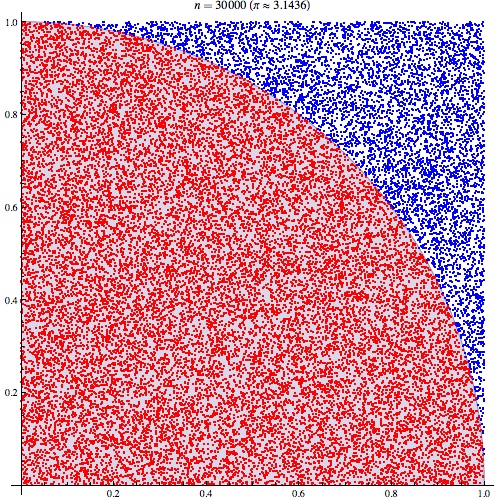
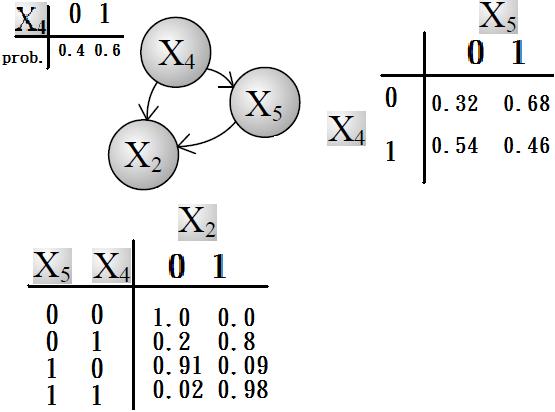
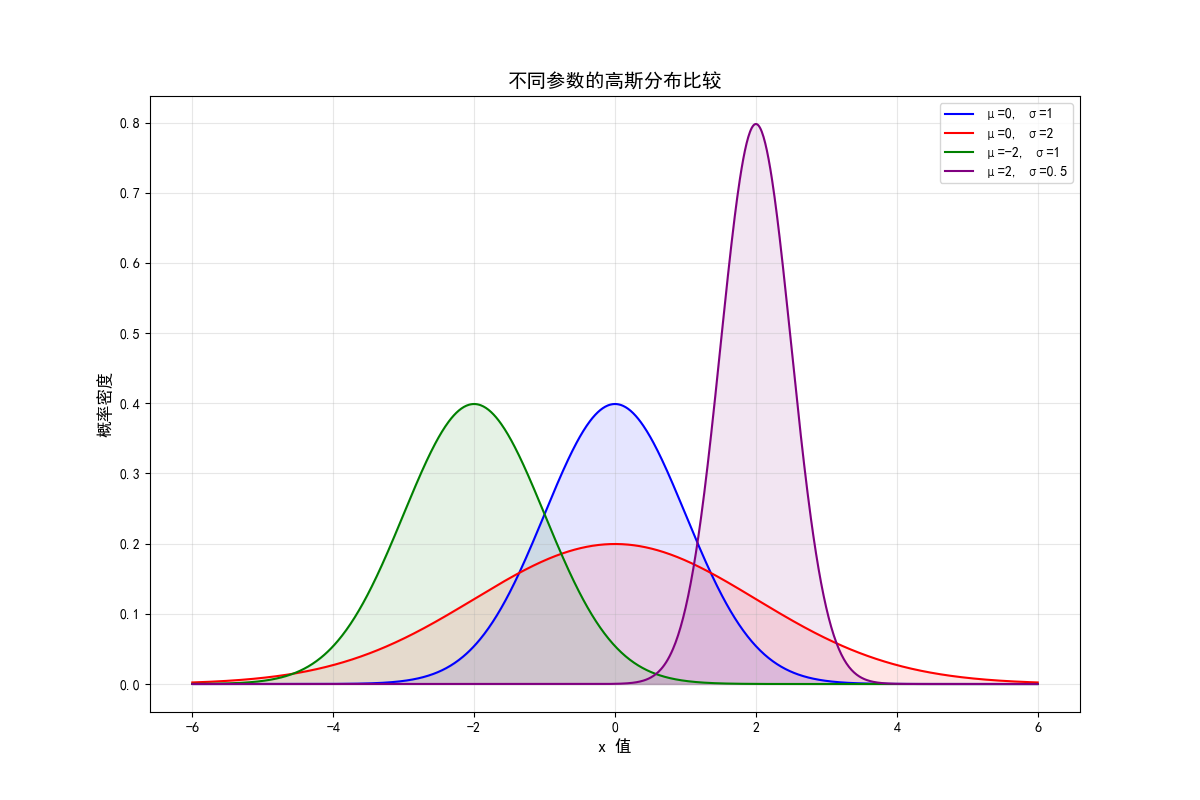
高斯分布的非线性封闭性
3. 如果
情形1:不同变量
设
定义:
这个
直接相乘:
注意常数项:
其中
把两部分二次型加起来:
正好等于:
因为块对角矩阵的逆仍然是块对角形式:
于是:
这正好就是:
也就是说,独立的两个高斯的乘积,等于它们拼成的联合高斯分布
情形2:同一变量
若
则
其中
首先,关注指数项:
令
则有
代回去得到
因此
即
从而证明了“成比例于高斯”
4.
边缘封闭性:如果
设联合高斯向量
则边缘分布
使用特征函数进行证明
联合高斯向量
令
边缘
这正是均值
证明:边缘
设随机向量
边缘分布
随机变量
代入边缘分布
交换积分顺序:
注意这里没有
这正是联合特征函数
5.
条件封闭性:如果
结论:
设联合高斯
并假设
由Schur补可得
联合密度为
把
对
因此
这说明
All articles on this blog are licensed under CC BY-NC-SA 4.0 unless otherwise stated.