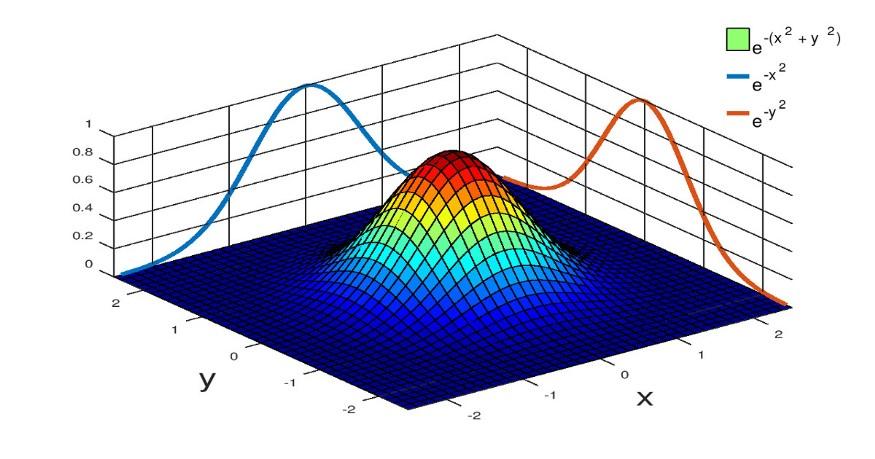
高斯分布的线性封闭性

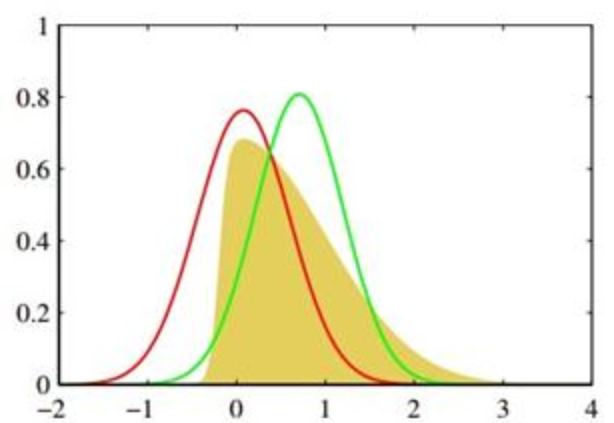
高斯分布的线性封闭性

1. 如果是高斯分布, 那么也是高斯分布

设 是一个服从高斯分布的随机向量，其均值为 ，协方差矩阵为 ，则的PDF为：

现在，考虑一个新的随机变量 ，其中 是一个矩阵， 是一个向量，我们要证明 也是一个高斯分布

计算 的均值

根据期望的线性性质，我们计算出 的均值 ：

计算 的协方差矩阵

接下来，计算 的协方差矩阵 ：

是常数矩阵，可以移到期望符号外： 又因为：

证明 的 PDF 形式符合高斯分布

使用特征函数证明线性变换下的高斯分布的特征函数仍然是高斯分布的形式

的特征函数为： 的特征函数为： 令 ，我们可以发现 实际上就是 的特征函数 ：

这个最终形式的特征函数，正是均值为 、协方差矩阵为 的高斯分布的特征函数。因为特征函数唯一地确定了概率分布，所以： 仍然服从高斯分布。

2. 高斯分布的线性组合也是高斯分布

以两个相互独立的高斯随机变量 和 为例进行证明，设 ，目标是证明 也是一个高斯随机变量

一个服从高斯分布 的随机变量，其特征函数为：

利用特征函数的定义来计算 的特征函数 ： 由于 和 相互独立，它们的指数函数的期望可以分开相乘：

将高斯分布特征函数表达式代入上式：

我们得到的 形式为 ，这正是高斯分布的特征函数形式。

因此， 也是一个高斯随机变量。其均值和方差分别为： 即： 这个结论可以推广到任意数量相互独立的高斯随机变量的线性组合