高斯分布

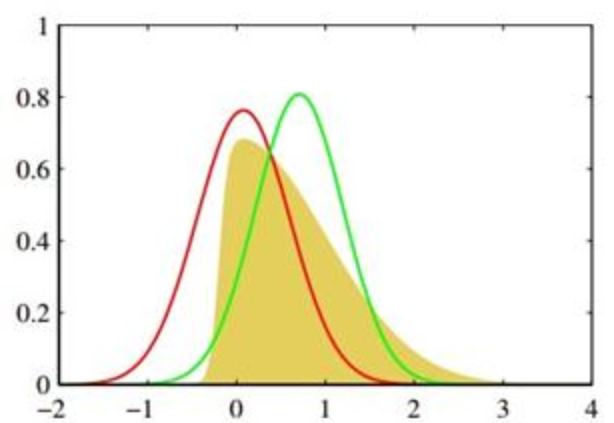
一维高斯分布

一维高斯分布的概率密度函数（PDF）呈钟形：

  • 均值 ：决定了钟形曲线的中心位置
  • 方差 ：决定了钟形曲线的胖瘦程度

公式为：

用符号 来表示随机变量 服从均值为 、方差为 的高斯分布

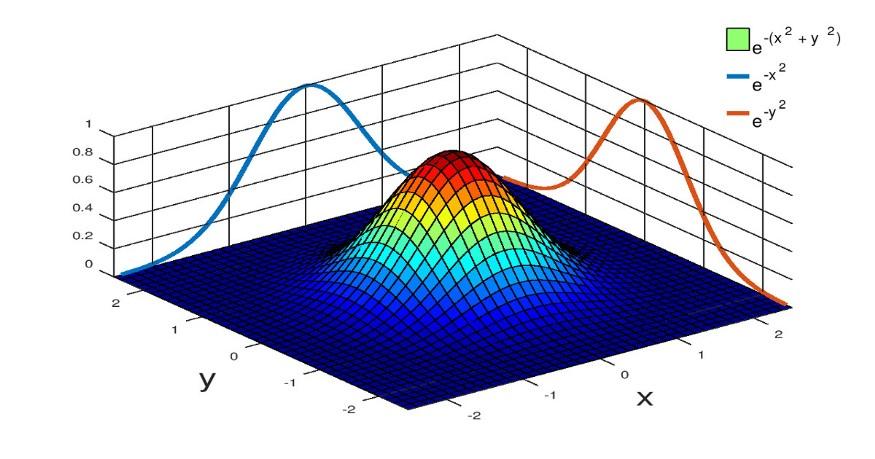
二维高斯分布

二维高斯分布的形状由以下参数决定：

  • 均值向量 ： 表示分布的中心点在平面上的位置
  • 协方差矩阵 ：描述了两个维度之间的方差和协方差关系

二维高斯分布的概率密度函数公式为：

是一个二维数据点， 是协方差矩阵的行列式。

维高斯分布（多元高斯分布）

多元高斯分布由以下参数决定：

  • 均值向量 ：一个 维向量，表示分布的中心
  • 协方差矩阵 ： 一个 的对称正定矩阵，对角线元素是各维度的方差，非对角线元素是协方差

维高斯分布的概率密度函数公式为：

这里， 是一个 维数据向量

特别地，VAE中出现的都是对角矩阵

高斯分布的特征函数

推导核心：配方法(completing the square) 来求解积分

推导 的特征函数

定义和初始设置

  • n维高斯分布的 PDF：

  • 特征函数的定义：

积分代入和准备

将 PDF 代入特征函数的定义中： 将常数项移到积分号外：

关键步骤：配方法

目标：配平方积分内部的指数部分

核心想法：整理成一个标准的高斯分布积分的形式，再加上一个与 无关的常数项

展开指数部分：

将所有包含 的项合并：

注意： 常数 常数

现在引入一个新的均值向量 ，希望将上式的前两项凑成 的形式

展开这个新形式：

通过比较 的系数项，我们得到：

因此，新的均值向量为：

现在，将指数部分重新写成配方后的形式：

将 代入： 展开：

由于 和 都是标量，所以

这就是我们需要的与 无关的常数项

求解积分

现在，我们将指数部分替换回积分中：

与 无关的常数项可以移出积分：

注意到积分号内部的项，正是均值为 ，协方差矩阵为 的高斯分布的 PDF,根据概率密度函数的性质，其在整个定义域上的积分为 1

最终结论

因此，整个表达式变为：