蒙特卡洛方法与链式法则

蒙特卡洛方法

核心思想：利用随机抽样逼近期望值

蒙特卡洛方法利用随机抽样来近似计算一个量的期望值，从而解决该量的数值问题，这个量通常是积分

假设我们想要计算一个函数 在某个概率分布 下的期望值 ：

当这个积分很难直接计算时，蒙特卡洛方法提供了一种近似解法

• 从概率分布 中独立地抽取 个样本点：
• 利用这些样本点来近似期望值：

被称为蒙特卡洛估计量

大数定律

根据大数定律（Law of Large Numbers），当样本数量 时，样本均值会收敛到期望值：

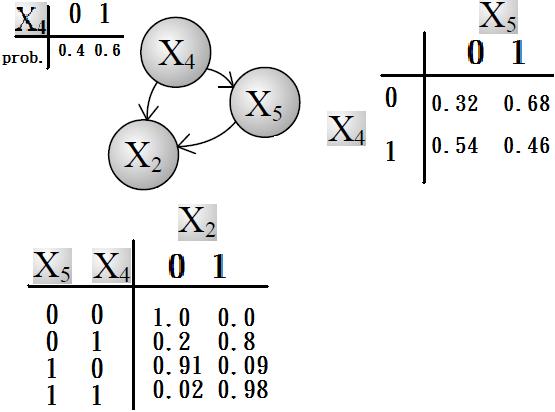
链式法则

假设我们有两个随机变量 和 ，它们的联合概率 可以表示为： 或者

这两种形式是等价的，根据条件概率的定义 很容易推导出来。

推广

对于多个随机变量 ，它们的联合概率 可以通过链式法则分解为：

更一般的形式是：

特别地，这里的 就是