贝叶斯估计

核心：把参数本身也看作是随机变量

  • 在最大似然估计中，模型参数被认为是一个固定但未知的值，我们通过数据来“猜”出它最可能的值
  • 而在贝叶斯估计中，我们认为参数是一个服从某个概率分布的随机变量,这个概率分布描述了我们对所有可能取值的信念（belief）

过程: 先验信念 + 观测数据 后验信念

这三个关键概念分别对应：

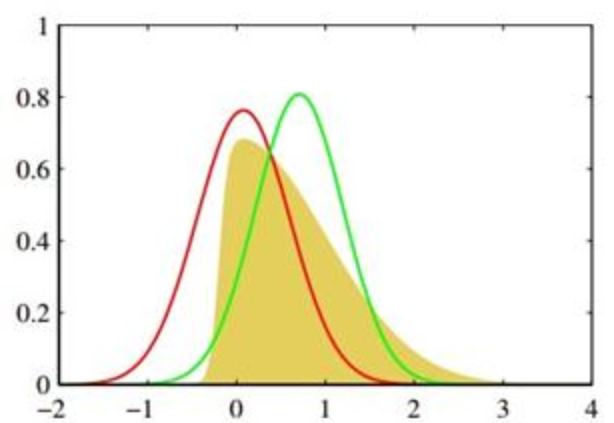
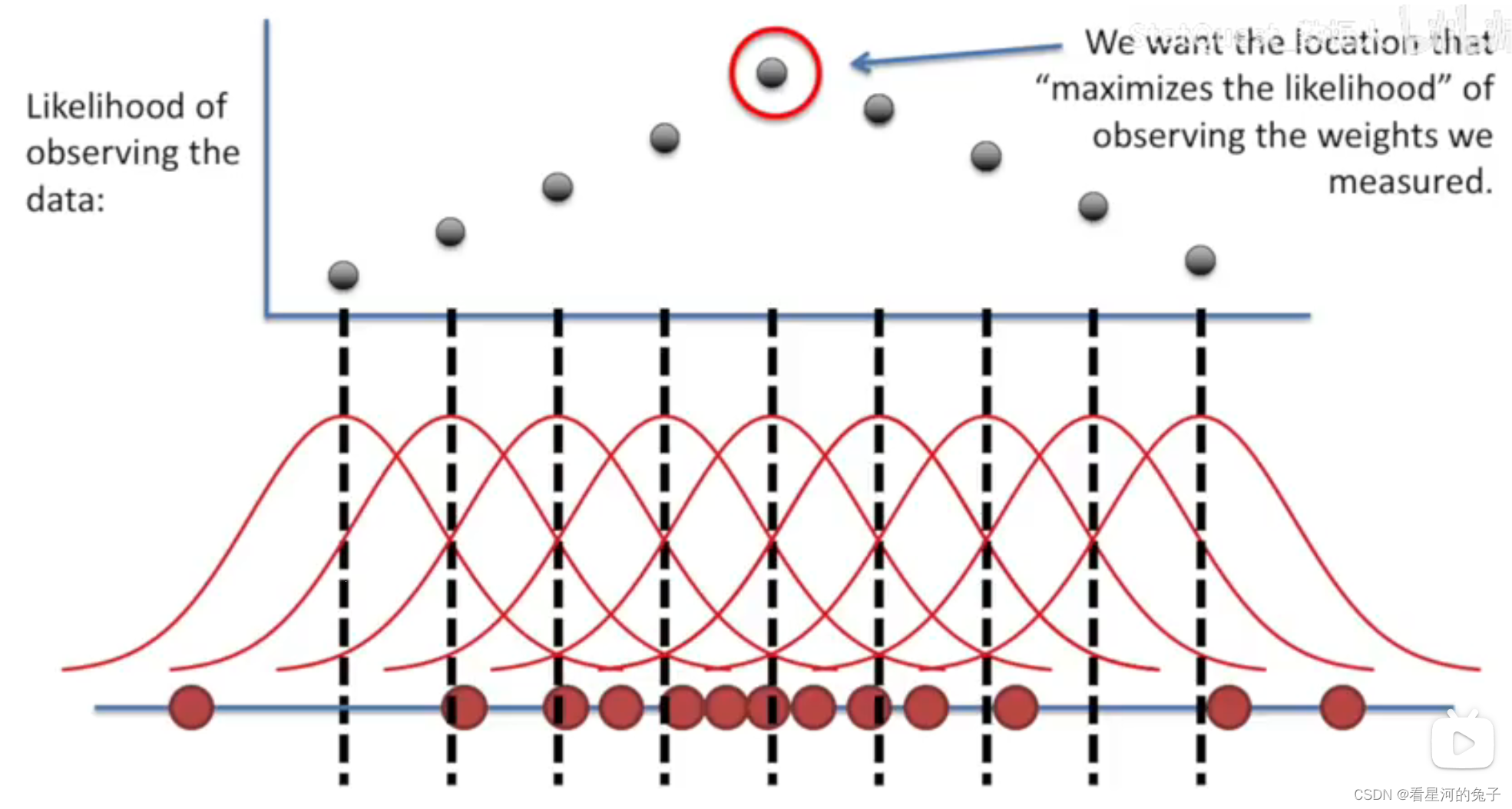
  • 先验分布 (Prior Distribution) ：在看到任何数据之前，我们对参数 的初始信念,反映了我们对参数的先验知识或经验
  • 似然函数 (Likelihood Function) ：和最大似然估计中的似然函数是同一个概念,描述了在给定参数 的情况下，观察到现有数据 的概率。
  • 后验分布 (Posterior Distribution) ：在观察到数据 之后，我们对参数的更新后的信念,结合了先验信念和数据提供的新信息

这三者之间的关系由贝叶斯定理(Bayes’ Theorem)来描述： 其中：

  • ：后验分布
  • ：似然函数
  • ：先验分布
  • ：边缘似然(Marginal Likelihood)，用于对后验分布进行归一化

因此，贝叶斯定理可以简化为： 这意味着：后验分布正比于似然函数乘以先验分布

贝叶斯估计提供了一种更灵活、更能融入先验知识的参数估计框架，更适用于数据稀缺的场景

利用贝叶斯估计缓解最大似然估计的局限性

在贝叶斯估计中，我们通常使用后验分布的众数(Maximum A Posteriori, MAP)作为点估计： 对比 MLE 的优化目标： 可以看出，贝叶斯估计的优化目标比 MLE 多了一项 ,这一项正是正则化项