Hongbo Ma's Blog

分数视角 参考文献 Papers Score-Based Generative Modeling Through Stochastic Differential Equations Generative Modeling by Estimating Gradients of the Data Distribution Sliced Score Matching: A Scalable Approach to Density and Score Estimation A Connection Between Score Matching and Denoising Autoencoders Estimation of Non-Normalized Statistical Models by Score Matching Blogs Generative Modeling by Estimating Gradients of the Data Distribution Sliced Score Matching: A Scalable Approach to Density a...

能量视角 参考文献 Papers Implicit Generation and Modeling with Energy-Based Models Maximum Entropy Generators for Energy-Based Models Blogs 能量视角下的GAN模型（三）：生成模型=能量模型 能量视角下的GAN模型（二）：GAN＝“分析”＋“采样” 能量视角下的GAN模型（一）：GAN＝“挖坑”＋“跳坑” 从能量视角下的GAN开始 能量模型 (EBM) 的定义 能量模型 将数据样本 映射到一个标量“能量”值 ，它对应于数据的一个非归一化估计密度函数 的负对数，即： 其中， 是归一化常数： 最大似然估计的梯度推导 训练 EBM 的目标：最大化训练数据的对数似然 ，这等价于最小化负对数似然 是常数 现在，我们对参数 求梯度： 正相负相 即： 正相负相 用生成器 替换 MCMC 采样 基于能量模型 的训练目标通常需要从模型自身的复杂分布 中采样（即 ），由于 难以采样，由神经网络 参数化的近似分布 来替代 采样 所以训练目标变为：...

Diffusion的数学推导与具体实现 参考文献 Denoising Diffusion Probabilistic Models Deep Unsupervised Learning using Nonequilibrium Thermodynamics 1.DPM Diffusion的前向过程(Forward Process) 前向过程是一个固定的马尔可夫链，它逐步向数据中添加高斯噪声，直至数据完全变成纯噪声,即代表的过程 用数学公式表示如下： 其中， 是真实数据样本， 是在每个时间步 添加的噪声方差， 构成一个固定的方差调度表 前向过程的关键特性 通过重参数化，可以在任意时间步 闭式地得到 的采样，而无需逐步迭代 定义 和 则对上文公式进行重参数化有： 代入 的表达式: 继续代入到: 然后根据高斯分布的封闭性以及推导公式，最终高斯分布参数为: 最终可以得到一个简洁的闭式形式： 这个公式是训练阶段的核心，它可以直接从原始数据 采样出任意时间步 的加噪样本 Diffusion的反向过程(Reverse Process) 反向过程是一个由模型学...

WorldScore: A Unified Evaluation Benchmark for World Generation Overview (1)统一性：将世界生成任务归纳拆解成了相机位姿变化下的下一场景生成任务，由此将3d生成，4d生成，视频生成等等世界生成方法统一化了 (2)测试维度： 可控性(controllability) 质量(quality) 动态性(dynamics) (3)大规模，多样的测试示例：3,000 个高质量的测试示例；涵盖了各种世界，包括静态和动态、室内和室外、照片写实和风格化景 挑战 视频生成、3D 场景生成和 4D 场景生成初是为特定任务设计，虽然具备作为“世界生成系统”的潜力，但是在世界生成概念扩展的今天，难以适应既能够无缝集成多个不同场景(综合性)，又能够具有详细空间布局控制(控制性)的任务需求。 解决这个问题，首先需要的就是一个benchmark！ 现有benchmark的缺陷 视频生成方向 评估仅限于单个场景，无法衡量模型在生成多场景、具有复杂空间关系的“世界”时的能力 3d,4d场景生成方向 评估基准缺少关键组件(如摄像机规格和...

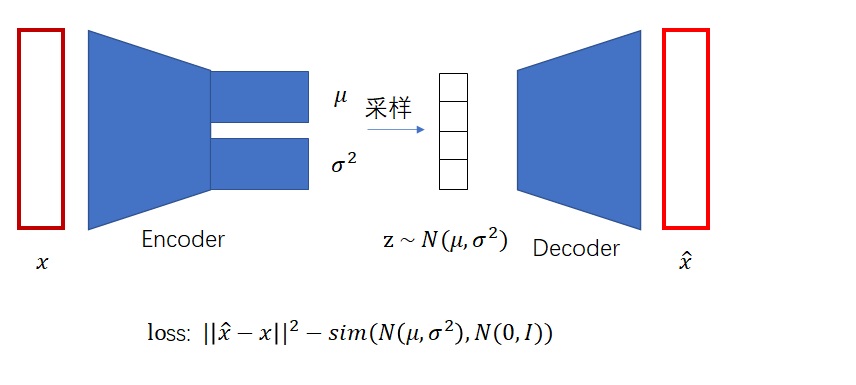
VAE的应用以及理论依据 训练后的两种应用 1. 直接生成 (Direct Generation) 如何操作？ 此时可以抛弃 encoder 从一个先验分布 （通常是标准正态分布）中采样 Z 通过解码器（decoder）做一个映射 ，也就是生成图像 为什么可以这样做？ 因为在 VAE 模型的优化过程中，encoder 的近似后验分布 和先验分布 已经被拉得比较接近 2. 重构原来的图像 (Reconstruction) 如何操作？ 此时需要同时使用 encoder 和 decoder 首先，基于 encoder ，对输入图像 X 进行编码，得到潜在表示 Z 然后，基于 decoder ，利用得到的潜在表示 Z，生成重构图像 目的？ 验证 VAE 是否能够学习到对数据的有效压缩和解压表示 确保模型能够将输入数据映射到潜在空间，然后再从这个潜在空间中准确地恢复出原始数据，这通常是评估 VAE 训练效果的一个重要指标 理论依据 高斯分布+CDF逆变换拟合任意分布 假设： 随机变量 服从标准正态分布 它的CDF（累积分布函数）记为 第一步：高斯...

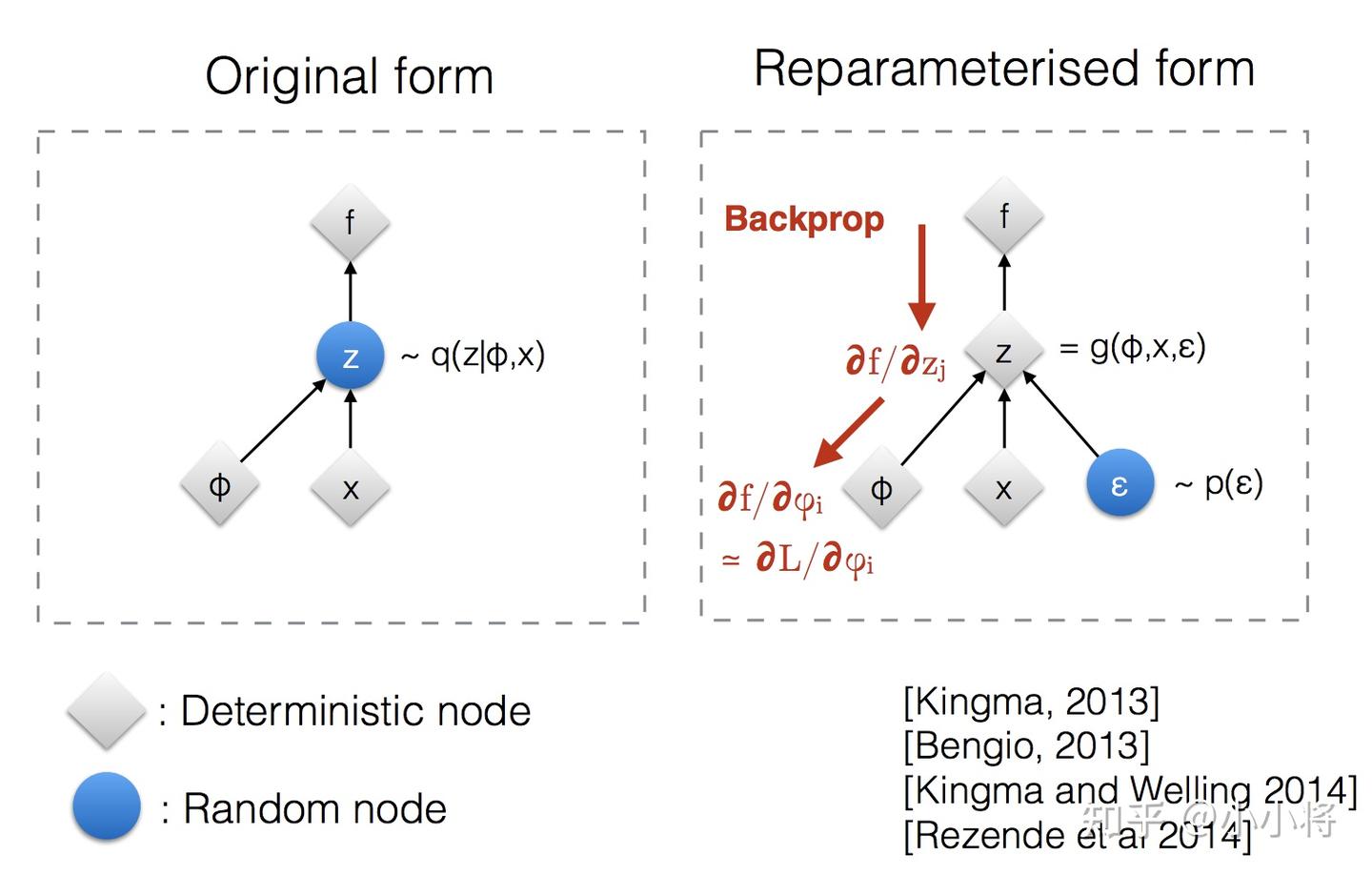
VAE的前向过程及核心代码 ELBO 目标函数： 代入建模： 第一项第二项 对 求导的思路 对 求导是相对简单的因为 只存在于第一项的对数似然项中，可以常规地进行梯度下降 对 求导的思路 第一项（重建损失）： 由于期望的分布本身依赖于参数 ，直接求导无法进行反向传播,因此，需要使用 “重参数化（reparameterization）” 技巧来解决 “变换之前”：我们从一个由 参数化的分布中直接采样潜在变量 ，即 ，这个过程不可导 “变换之后”：我们引入，通常从标准正态分布中采样，即 。然后，将 转换为潜在变量 ： 求导问题：通过重参数化，原来的期望 就变成了对 的期望 可以将梯度符号 “穿过” 期望符号 ， 第二项（KL 散度）： 这一项可以进行显式计算，即当 和 都为高斯分布时，KL 散度有一个解析解 计算思路 最后计算的式子为： 应用蒙特卡洛（Monte Carlo, MC）方法： 从标准正态分布 中，采样出若干个随机变量 利用采样得到的 ，通过重参数化公式 计算得到潜在变量 计算近似 ELBO： 通过反向传播对 和 求导，...

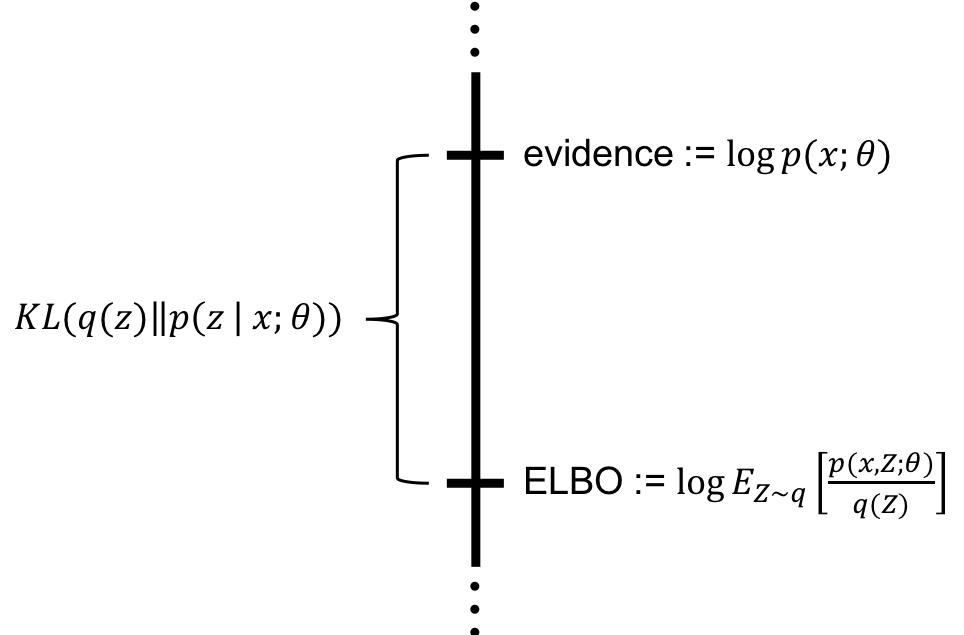
ELBO 是我们想要计算的边缘似然（Evidence），它表示观测数据 出现的概率 引入变分分布 ，对真实后验分布 进行近似 同时将上述的积分式转化为一个可以简单计算的形式 将积分形式转化为期望形式，便于下一步的计算 应用Jensen不等式，将等号变成了大于等于号 就是证据下界（ELBO） 在VAE中，我们的目标就是最大化这个下界（ELBO），因为最大化下界也就意味着我们尽可能地最大化原始似然 。这个最大化的过程，同时会优化我们的编码器（Encoder）和解码器（Decoder） 理解ELBO：变分推断 对于任意的 ，有： 其中： 它表明我们想要计算的边缘似然 ，可以精确地分解成两部分之和： ：变分下界（ELBO），这是我们可以计算和最大化的部分。 ： 和真实后验分布 之间的KL散度，衡量两个分布之间距离 证明如下： 参数化：，在实践中，我们通常参数化来优化，将其定义为一个由参数 决定的神经网络 ：通过调整 的参数 ，来最大化变分下界 。当我们最大化 时，我们实际上是在让 尽可能地接近真实的后验分布 ，从而使KL散度项趋近...

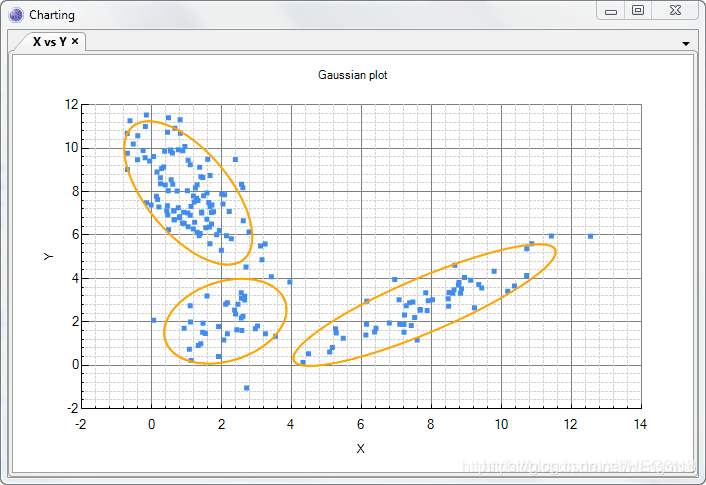
VAE的概率建模 对于一个图像来说，可以认为它对应这一套隐空间中的编码,在确认的时候，对应的分布就是相同的，而就是在这个分布之中采样得到 把这个隐空间学好了，就可以对于生成的东西有更好的操控 把学好了，可以直接采样,这个分布很容易进行sample，首选还是多维高斯分布 建模 生成式模型的概念建模方式 参数化单个样本 VAE: 这个优化非常困难 生成式模型的概念建模本质 无数个高斯模型的混合 每个图像X，都有一个对应Z编码，再对应一个该图像的分布 sample： 为何难以优化 log难以穿过积分号 既然难以计算，一种想法是通过蒙特卡罗方法来取近似，即从先验分布 中随机采样大量的 ，然后用 来近似这个积分，但是这么做的问题在于： 是一个非常简单的分布（如标准正态分布），但能够生成有意义图像 的 向量，在整个 的空间里只占极小的、几乎可以忽略的区域，所以如果随机采样，会采样到大量的噪声 直接来 sample ， 的概率大多为0，导致模型一直 error 很大，很难拟合样本 模型学习不到有意义的东西 解决思路：我们要更加有效的 ，最好使用 ...

隐变量与隐空间 隐变量就是那些我们无法直接观测，但会影响观测数据的变量。 它们存在于模型里，用来解释或生成观测到的数据。 用一句话总结：观测不到，但背后起作用的“隐藏因素” 数学表达 在概率模型里： 观测变量：（我们能看到的数据，比如图片、文本、声音）。 隐变量：（不能直接看到的结构，比如图片里的语义标签、风格因子）。 联合分布写成： 如果我们只关心观测数据 ，就需要边缘化掉隐变量： 对于隐变量的一些基本假设 在含有隐变量的概率模型中，一个完整的数据点不只是观测到的 ，还包括生成它的隐变量 ，即一个完整的数据点是 每个样本对应一个隐变量,即对于观测到的数据 ，在生成模型里都假设有某个潜在的 在起作用 我们只能观测到， 是观测不到的，通常是数据(比如图片像素), 是抽象的潜在因子（比如姿态、表情、光照） 因为对 积分往往不可解，直接去优化 是困难的 所以使用分解：，即观测数据 的分布由“给定隐变量的条件分布”与“隐变量的先验”相乘后积分(求和)得到 一旦知道了， 或者 是容易优化的 生成模型中的隐变量 隐变量 在生成模型里起决定性作用。 表示“从隐变量到...

泛函与变分 泛函（functional） 输入：一个 函数 输出：一个数（标量） 泛函本质上就是 作用在函数域上的“函数” 常见例子 积分型泛函 输入一个函数 ，输出它在区间 上的积分 带权积分泛函 这是变分法里常见的泛函，输入函数 ，输出一个实数 点值泛函 输入函数 ，输出它在某个点 的值 变分 变分类似，但是它处理的是函数的函数，也就是泛函（functional） 泛函：把函数作为输入，输出一个数的对象。例如： 这里 是一个函数， 是一个数 变分问题：找出哪个函数 能让 最大或最小 人工神经网络本质上在进行变分 给定量集合 Loss就是一个泛函 在函数空间 中做泛函的极小， 是连续函数的空间，无穷维 参数化 选定参数空间是人工神经网络形式的函数 ， 是一层人工神经网络变换， 是全部的人工神经网络参数 有限维空间中求解 VAE中进行的变分 上述式子对于任意PDF 均成立，即自变量为所有PDF的函数空间 泛函为：